Cryptography - One-time Pad, Information Theoretic Security, and Stream Ciphers

WARNING

One-time Pad和数学基础的部分（从英文幻灯片的第1页至第16页，第22至第24页）被略过了。

信息论安全性 (Information-Theoretic (Shannon) Security) = 完善保密性 (Perfect Secrecy)

WARNING

完善保密性(perfect secrecy)是信息论安全性的一个特例，为香农提出的信息学观点，具有该性质的密文不应该透露任何明文的信息。达成这项性质的方法是使用与明文空间相等或更大的密钥空间。完善保密性 - wikipediaopen in new window

基本思想：密文不应透露关于明文的任何“信息”。

[定义] 一个密码系统在信息空间(Message space) $M$ 上的加密是具有完善保密性(Perfect Secrecy)的，如果：

对于 $M$ 上的所有概率分布

对于任意一个在空间 $M$ 上的信息 $m$

对于任意一个在密文空间 $C$ 上，满足 $P r [C = c] > 0$ 的密文 $c$

均有 $P r [P T = m ∣ C T = c] = P r [P T = m]$

定义中的参数

$P r [P T = m]$ 是攻击者/对手(adversary)在看到密文之前认为明文是 $m$ 的概率。
$P r [P T = m ∣ C T = c]$ 是对手知道密文 $c$ 后，认为明文是 $m$ 的概率。
Pr[PT=m|CT=c] = Pr[PT=m]代表着攻击者知道密文是c$之后，他对明文是什么的看法并没有改变。

对完善保密性的一个等价定义

[定义] 一个加密方案是具有完善保密性的，当且仅当对于任何密文 $c$ ，以及任意的两个明文 $m 1 $ 和 $m 2 $ ， $m 1 $ 被加密为 $c$ 的概率与 $m 2 $ 被加密为 $c$ 的概率相同。

数学表述为：

$\forall$ message $m 1$ , $m 2$

$\forall$ ciphertext $c$

$P r [C T = c ∣ P T = m 1] = P r [C T = c ∣ P T = m 2]$

另一个对完善保密性的等价定义

如果对 $M$ 上任意的概率分布，随机变量 $P T$ and $C T$ 是独立的，则一个定义在信息空间 $M$ 上的加密方案是具有完善保密性的，也即：

$\forall$ message $m \in M$

$\forall$ ciphertext $c \in C$

$P r [P T = m \land C T = c] = P r [P T = m] \cdot P r [C T = c]$

注意到这等价于：当 $P r [C T = c] \neq 0$ 时，有：

$P r [P T = m] = P r [P T = m \land C T = c] / P r [C T = c] = P r [P T = m ∣ C T = c]$

这也等价于：当 $P r [P T = m] \neq 0$ 时, 有：

$P r [C T = c] = P r [P T = m \land C T = c] / P r [P T = m] = P r [C T = c ∣ P T = m]$

信息论安全性的一个例子

考虑对一个六面骰子（点数为1-6）的投掷结果进行加密。
- 方法1：随机生成K=[1...6]，将骰子的读数+K作为密文。
  - 问题：明文的分布是什么？
  - 问题：在看到密文为3后，明文可能是什么；在看到密文为12后，明文可能是什么？
- 方法2：随机生成K=[1...6]，将骰子的读数+K，然后对6取模作为密文。
  - 考虑方法1中的两个问题。
  - 是否可以用暴力攻击的方法破解加密？

完善保密性 (Perfect Secrecy)

当密码中的密钥被均匀地选择时，该密码具有完善保密性，当且仅当对任何(M,C)来说，将M加密到C的密钥数量是相同的。
- 这意味着 $\forall c \forall m 1 \forall m 2 P r [C T = c ∣ P T = m 1] = P r [C T = c ∣ P T = m 2]$
当限制信息长度为定长时，一次性密码本(One-time pad)有完善保密性（证明？）

完善保密性的“坏消息”定理（The "Bad News" Theorem）

问题：在一次性密码本中，要求密钥和信息一样长是否是实现完善保密性的内在要求？
答案：是的，完善保密性意味着密钥的长度大于等于信息的长度。
这意味着在实践中，采用一次性密码本的加密方法难以实现完善保密性。

证明如下：

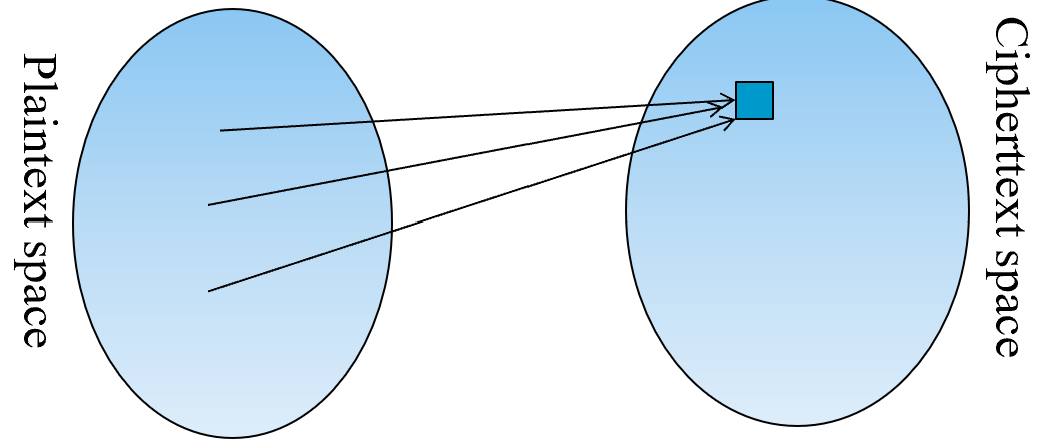bad_news 考虑到密文 $C 0 $ ，对于明文空间中的任意明文 $M$ ，必须存在至少一个密钥，在这个密钥的作用下密文 $C 0 $ 可以被解密为 $M$ 。此外，对于明文空间中任意的两个明文，它们所对应的密钥必须不同（否则人们无法唯一地解密密文）。因此，密钥的数量必须至少与明文的数量一样大。

问题：考虑明文空间、密文空间和密钥空间，对于任何加密系统，它们的大小必须满足什么关系？对于一个满足完善保密性的系统来说，它们的大小必须满足什么关系？

流密码 (Stream Ciphers)

在一次性密码本中，密钥是一个随机字符串，其长度至少与信息相同。
流密码：
- 基本思想：用“伪随机数”取代“随机数”。
- 使用伪随机数生成器(Pseudo Random Number Generator, abbr. PRG or PRNG)
- PRNG： ${0, 1} s \to {0, 1} n $
  - 伪随机数生成器将一个短的（如128 bit）随机种子扩展成一个较长的（如106位）、并且“看起来很随机的”字符串
- 密钥就是种子
- 基本加密方法： $E k e y [M] = M \oplus P R N G (k e y)$ ，其中 $\oplus$ 为按位的异或运算。

伪随机数生成器 (Pseudo Random Number Generator)

适用于密码学、仿真、随机算法等。
- 例如：流密码，生成会话密钥
相同的种子总是给出相同的输出流
- 问题：为什么这对流密码来说是必要的？
仿真需要均匀分布的序列
- 例如，具有一些统计学特性
在密码学意义上安全的(Cryptographically secure)伪随机数生成器需要不可预测的序列
- 能够通过“下一比特测试(next-bit test)”：给定输出的连续比特序列（但不是种子），下一比特必须难以预测
然而，有一些伪随机数生成器很弱：如果攻击者能够得到足够长度的输出序列，他可以通过这个输出序列来得到密钥。
- 不要将这些伪随机数生成器用于加密目的

随机性和伪随机性

对于一个良好的流密码，它需要是“伪随机”。
随机性不是一个字符串的属性
- 000000比011001更“不随机”吗？
- 随机性是一种分布的属性，或者是从分布中抽取的随机变量的属性
相似的，伪随机也是一个分布的属性
我们认为“I-长”字符串空间（即空间中每一个元素均是长度为 $I$ 的字符串）上的分布 $D$ 是伪随机的，如果它与随机分布无法区分(indistinguishable)。
我们使用“随机字符串(random string)”和“伪随机字符串(pseudorandom string)”简称满足上面条件的字符串。

区分器 (Distinguisher)

工作在两个分布上的区分器 $D$ 的工作方式如下：给予 $D$ 一个从两个分布中采样的字符串， $D$ 试图猜测它来自哪个分布，如果 $D$ 猜对了，那我们称 $D$ 成功了。

伪随机数生成器的定义

[定义3.14] 如果一个在输入长度为 $n$ 时，输出一个长度为 $l (n)$ 的字符串的算法 $G$ 满足：

对于每个 $n$ ，均有 $l (n) \geq n$ 。
对于每个区分器 $D$ （原文：For each PPT distinguisher $D$ ，能力有限的），均存在一个可忽略的函数 $n e g l$ ，使得 $∣ P r [D (r) = 1] - P r [D (G (s)) = 1] ∣ \leq n e g l (n)$ （其中 $r$ 从 ${0, 1} l (n) $ 中均匀地随机选择， $s$ 从 ${0, 1} n $ 中均匀地随机选择。

则我们称算法 $G$ 是一个伪随机发生器。

使用流密码进行加密的安全性

考虑构造加密 $Π$ ，以及对 $m$ 的加密 $G (k) \oplus m$ 。

[定理3.16] 如果 $G$ 是一个伪随机生成器，那么 $Π$ 在有窃听者(EAVesdropper)的情况下有不可区分的加密(indistinguishable encryption)。

对定理3.16的证明如下：

如果 $Π$ 在有窃听者的情况下不存在不可区分的加密，那么存在攻击者A，可以以不可忽略的概率 $O (ϵ)$ 破解 $Π$ 。我们构建一个区分器D如下：

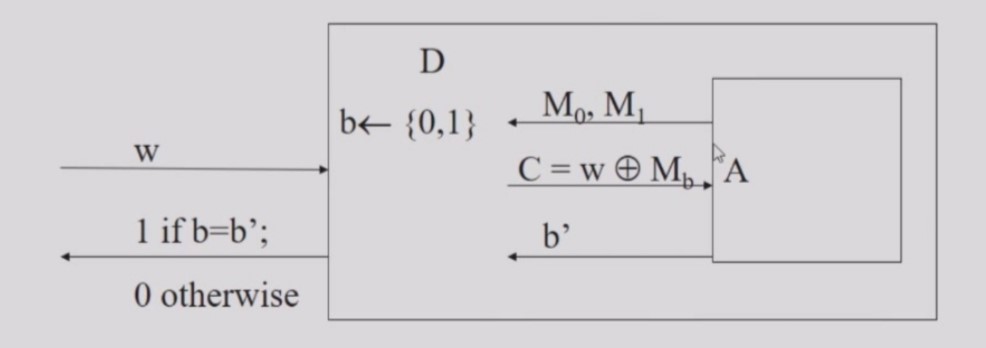
Them_3_16

[定理] $G (k) \oplus m$ 是防窃听(EAV-secure)的，如果 $G$ 是一个伪随机数生成器。

EAV-secure（防窃听）: 攻击者A任意挑选两条不同的信息 $m 0 , m 1 $ （可以挑选无限次）作为明文提供给挑战者Ch，挑战者选取其中的随机位 $b$ ，将使用密钥 $s k$ 加密得到密文 $E n c s k (m b )$ 中的第 $b$ 位，返回给攻击者A，攻击者需要猜测位数 $b$ 。如果攻击者能够猜测正确 $b$ ，那么这个加密算法是不防窃听的。即破解者始终能够破解其中的某几位。
- 攻击者A：可证明安全中试图解决攻破方案的假想攻击者
- 挑战者Ch：可证明安全中试图解决困难问题的挑战者
```
+----+     pp      +---+
| Ch | ----------> | A |
+----+    m0, m1   +---+
  sk   <---------- m0, m1
   b   Enc(sk,m_b)     
       ---------->
            b'
       <----------
```
- 在上面的示意图中，Ch指挑战者，它会裁判A的破解答案，并判断A是否成功破解这个加密算法。pp指公共参数(Public Parameter)，它是一组已知的值或变量，并在加密系统的参与者之间公开共享，这些参数通常包括公钥、系统参数或其他加密算法运行所需的变量等值，在这里可以理解为加密算法。
- 可以从这个链接（CS555，Lecture20，Spring17，PU）open in new window获得更多信息。

反证如果存在一个攻击A能够破坏 $G (k) \oplus m$ 的防窃听，那么我们就可以构造一种攻击B（一种规约），它能够破坏伪随机数生成器 $G$ 的伪随机性。

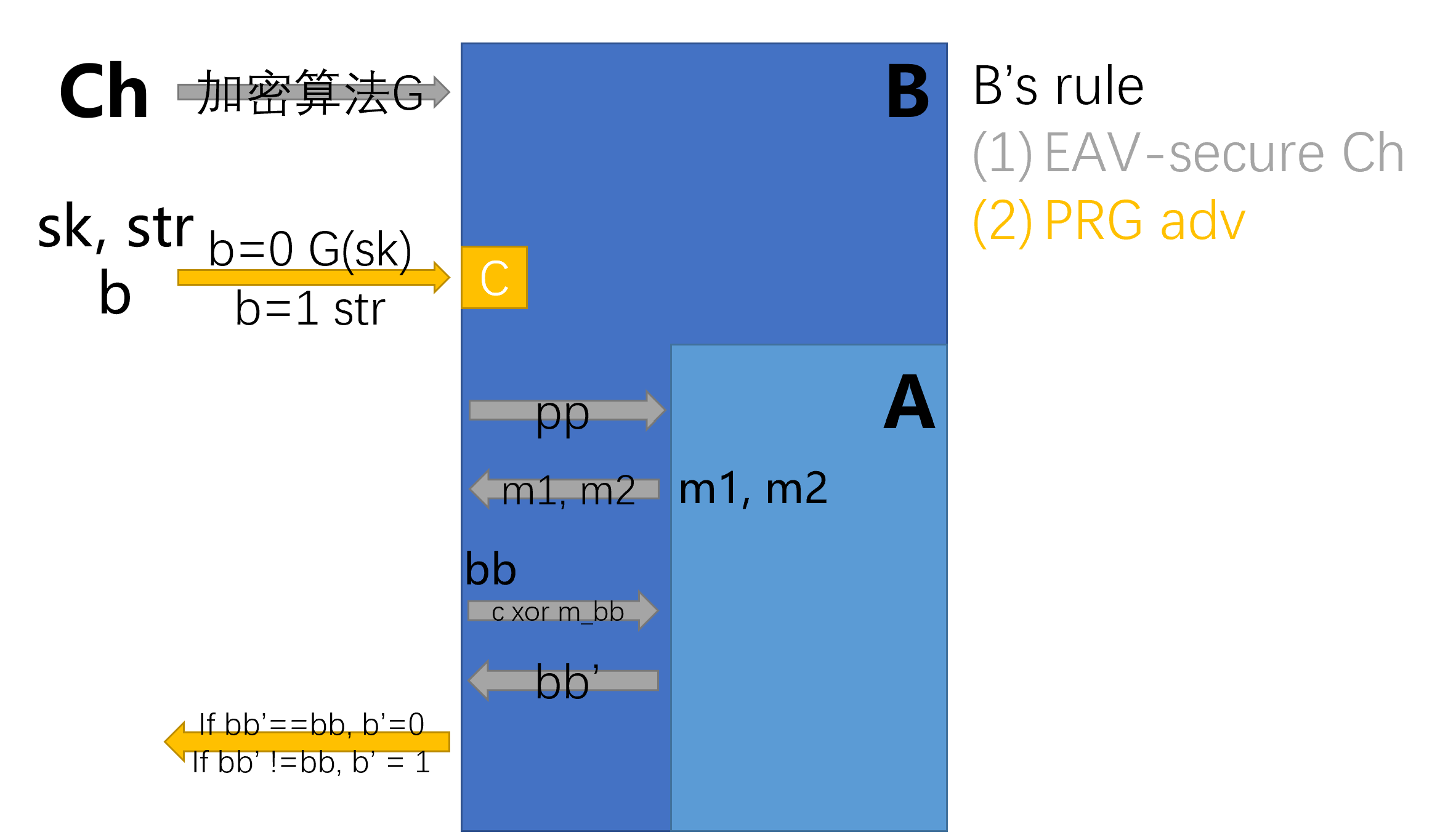
Use_B_attck_G

证明攻击A持有 $ϵ$ 的概率（不收敛至0）破坏 $G (k) \oplus m$ 的防窃听，那么根据上图构造的攻击B打破伪随机数生成器 $G$ 的伪随机性的概率是

$ P r [B w i n s] = P r [B w i n s ∣ b = 0] \cdot P r [b = 0] + P r [B w i n s ∣ b = 1] \cdot P r [b = 1] = P r [B w i n s ∣ b = 0] \cdot 0.5 + P r [B w i n s ∣ b = 1] \cdot 0.5 = P r [b ' = 0 ∣ b = 0] \cdot 0.5 + P r [b ' = 1 ∣ b = 1] \cdot 0.5 \geq (0.5 + ϵ) \cdot 0.5 + 0.5 \cdot 0.5 = 0.5 + 0.5 \cdot ϵ $

流密码的特性

典型的流密码运行速度非常快
被广泛使用，但在应用中进程存在漏洞
- 内容扰乱系统，一种加密光盘盘片的方式：错误地使用线性反馈移位寄存器(Linear Feedback Shift Registers)
- 有线等效加密(Wired Equivalent Privacy, abbr. WEP)，又称无线加密协议(Wireless Encryption Protocol, abbr. WEP)：错误地使用了RC4
- SSL：使用RC4的SSLv3没有已知的重大缺陷

流密码的安全性质

在已知明文、选择的明文或选择的密文的情况下，攻击者知道密钥流（即 $P R N G (k e y)$ ）。
- 安全性取决于 $P R N G$
- $P R N G$ 必须是“不可预测的(unpredictable)”
问题：流密码有完善保密性吗？
问题：如何以暴力方式破解流密码？
如果同一个密钥流被使用两次，那么流密码很容易被破解。
- 这是流密码的一个基本弱点，即便在流密码中使用的PRNG很强，仍然存在这个问题。

流密码的应用方式

如果同一个密钥流被使用两次，那么流密码很容易被破解。
- 这是流密码的一个基本弱点，即便在流密码中使用的PRNG很强，仍然存在这个问题。
在实际应用中，同一个密钥被用来加密许多信息
- 例如在无线通信领域中
- 解决方案：使用初始化向量(Initial vectors , abbr. IV)。
- $E k e y [M] = [I V, M \oplus P R N G (k e y ∣ ∣ I V)]$
  - IV以明文的方式发送给接收方
  - IV需要完整性保护(integrity protection)，但不需要保密性保护(confidentiality protection)
  - IV能够确保加密时采用的密钥流不重复，但它不能不增加暴力攻击的成本
  - 在知道IV的情况下，如果没有密钥，密文仍然不能被解密
- 需要确保IV永不重复

针对选择的明文攻击(Chosen Plaintext Attack)的安全 - CPA安全

到目前为止考虑的安全概念(指One-side或EAV)是针对仅有密文的攻击者的安全概念
模拟选择明文攻击
- 攻击者可以选择明文并始终能够自适应地(adaptively)获得相应的密文
  - 自适应的意思是，攻击者可以查看第一个被选择的明文对应的密文，然后选择下一个明文，获得密文，以此往复
  - 在这种攻击模式中，攻击者可以事先任意选择一定数量的明文，让被攻击的加密算法加密，并得到相应的密文
- 如何模拟攻击者的这种能力？
  - 攻击者获得一个预言机，它可以对信息进行加密，但不泄露密钥

TIP

相比防窃听(EAV-Secure)，针对选择明文攻击的安全能够描述一个系统在加密多个明文时的安全性
一个显著的差异是，对于同一个密钥和加密来说，CPA安全保证了攻击者已知无论多少个密文时，他都不能找到这些密文的相关性，即这些密文不存在相关性

CPA安全(又称IND-CPA安全)

一个私钥加密方案 $Π = (G e n, E n c, D e c)$ 在选择明文攻击下具有不可区分的加密当且仅当对于所有能力有限的攻击者A，均存在一个可忽略的函数 $n e g l$ ，使得 $P r [P r i n K A, Π c p a = 1] \leq 1 / 2 + n e g l (n)$
问题：没有一个确定性加密(deterministic encryption)是CPA安全的，为什么？

CPA安全的性质

对于多明文信息的CPA安全等同于对于单个明文信息的CPA安全
如果已知一个固定长度的加密方案是CPA安全的，我们可以通过分别加密明文的不同部分来加密任意长度的明文

# Cryptography - One-time Pad, Information Theoretic Security, and Stream Ciphers

# 信息论安全性 (Information-Theoretic (Shannon) Security) = 完善保密性 (Perfect Secrecy)

# 定义中的参数

# 对完善保密性的一个等价定义

# 另一个对完善保密性的等价定义

# 信息论安全性的一个例子

# 完善保密性 (Perfect Secrecy)

# 完善保密性的“坏消息”定理 （The "Bad News" Theorem）

# 流密码 (Stream Ciphers)

# 伪随机数生成器 (Pseudo Random Number Generator)

# 随机性和伪随机性

# 区分器 (Distinguisher)

# 伪随机数生成器的定义

# 使用流密码进行加密的安全性

# 流密码的特性

# 流密码的安全性质

# 流密码的应用方式

# 针对选择的明文攻击(Chosen Plaintext Attack)的安全 - CPA安全

# CPA安全(又称IND-CPA安全)

# CPA安全的性质