Cryptography - One-time Pad, Information Theoretic Security, and Stream Ciphers

WARNING

Mathmatic foundations and One-time Pad (from slide01 to slide16, slide22 to slide 24) is omitted.

Shannon (Information-Theoretic) Security = Perfect Secrecy

Basic Idea: Ciphertext should reveal no “information” about Plaintext

Definition. An encryption over a message space $M$ is perfectly secure if:

$\forall$ probability distribution over $M$

$\forall$ message $m \in M$

$\forall$ ciphertext $c \in C$ for which $P r [C = c] > 0$

We have

$P r [P T = m ∣ C T = c] = P r [P T = m]$ .

Explanation of the Definition

- $P r [P T = m]$ is what the adversary believes the probability that the plaintext is $m$ , before seeing the ciphertext - $P r [P T = m ∣ C T = c]$ is what the adversary believes after seeing that the ciphertext is $c$ - $P r [P T = m ∣ C T = c] = P r [P T = m]$ means that after knowing that the ciphertext is C0, the adversary’s belief does not change.

An Equivalent Definition of Perfect Secrecy

Definition. An encryption scheme is perfectly secure if and only if for any ciphertext $c$ , and any two plaintext $m 1$ and $m 2$ , the probability that $m 1$ is encrypted to $c$ is the same as the probability that $m 2$ is encrypted to $c$ .

$\forall$ message $m 1$ , $m 2$

$\forall$ ciphertext $c$

$P r [C T = c ∣ P T = m 1] = P r [C T = c ∣ P T = m 2]$

Another equivalent definition

An encryption scheme over a message space $M$ is perfectly secure if $\forall$ probability distribution over $M$ , the random variables $P T$ and $C T$ are independent. That is,

$\forall$ message $m \in M$

$\forall$ ciphertext $c \in C$

$P r [P T = m \land C T = c] = P r [P T = m] \cdot P r [C T = c]$

Note that this is equivalent to: When $P r [C T = c] \neq 0$ , we have

$P r [P T = m] = P r [P T = m \land C T = c] / P r [C T = c] = P r [P T = m ∣ C T = c]$

This is also equivalent to: When $P r [P T = m] \neq 0$ , we have

$P r [C T = c] = P r [P T = m \land C T = c] / P r [P T = m] = P r [C T = c ∣ P T = m]$

Example for Information Theoretical Security

Consider an example of encrypting the result of a 6-side dice (1 to 6).
- Method 1: randomly generate K=[1..6], ciphertext is result + K.
  - What is plaintext distribution? After seeing that the ciphertext is 3, what could be the plaintext. After seeing that the ciphertext is 12, what could be the plaintext?
- Method 2: randomly generate K=[1..6], ciphertext is (result + K) mod 6.
  - Same questions.
  - Can one do a brute-force attack?

Perfect Secrecy

Fact: When keys are uniformly chosen in a cipher, the cipher has perfect secrecy iff. the number of keys encrypting M to C is the same for any (M,C)
- This implies that $\forall c \forall m 1 \forall m 2 P r [C T = c ∣ P T = m 1] = P r [C T = c ∣ P T = m 2]$
One-time pad has perfect secrecy when limited to messages over the same length (Proof?)

The “Bad News” Theorem for Perfect Secrecy

Question: OTP requires key as long as messages, is this an inherent requirement for achieving perfect secrecy?
Answer. Yes. Perfect secrecy implies that key-length $\geq$ msg-length
Implication: Perfect secrecy difficult to achieve in practice

Proof:

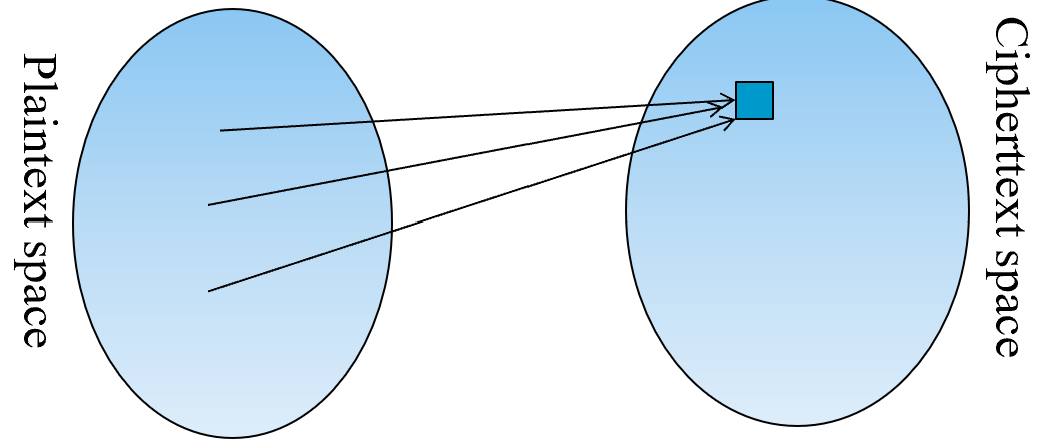bad_news Consider one ciphertext C0, for any plaintext M in the plaintext space, there must exist at least one key such that under the key C0 can be decrypted into M. Furthermore, for any two plaintexts, the corresponding keys must be different, because otherwise, one cannot uniquely decrypt the ciphertext. Hence, the number of keys must be at least as large as the number of plaintexts.

Consider the plaintext space, ciphertext space, and key space, what relations their sizes must satisfy, for any encryption system? What about for a system that satisfy perfect secrecy?

Stream Ciphers

In One-Time Pad, a key is a random string of length at least the same as the message
Stream ciphers:
- Idea: replace “rand” by “pseudo rand”
- Use Pseudo Random Number Generator
- PRNG: ${0, 1} s \to {0, 1} n $
  - expand a short (e.g., 128-bit) random seed into a long (e.g., 106 bit) string that “looks random”
- Secret key is the seed
- Basic encryption method: $E k e y [M] = M \oplus P R N G (k e y)$

Pseudo Random Number Generator

Useful for cryptography, simulation, randomized algorithm, etc.
- Stream ciphers, generating session keys
The same seed always gives the same output stream
- Why is this necessary for stream ciphers?
Simulation requires uniform distributed sequences
- E.g., having a number of statistical properties
Cryptographically secure pseudo-random number generator requires unpredictable sequences
- satisfies the "next-bit test": given consecutive sequence of bits output (but not seed), next bit must be hard to predict
Some PRNG’s are weak: knowing output sequence of sufficient length, can recover key.
- Do not use these for cryptographic purposes

Randomness and Pseudorandomness

For a stream cipher (PRNG) is good, it needs to be "pseudo-random".
Random is not a property of one string
- Is "000000" "less random" than "011001"?
- Random is the property of a distribution, or a random variable drawn from the distribution
Similarly, pseudo-random is property of a distribution
We say that a distribution $D$ over strings of length-I is pseudorandom if it is indistinguishable from a random distribution.
We use "random string" and "pseudorandom string" as shorthands

Distinguisher

A distinguisher D for two distributions works as follows: D is given one string sampled from one of the two distributions D tries to guess which distribution it is from D succeeds if guesses correctly

Pseudorandom Generator Definition

Definition 3.14. We say an algorithm $G$ , which on input of length $n$ outputs a string of length $l (n)$ , is a pseudorandom generator if

For every $n$ , $l (n) \geq n$
For each PPT distinguisher D, there exists a negligible function negl such that $∣ P r [D (r) = 1] - P r [D (G (s)) = 1] ∣ \leq n e g l (n)$ Where $r$ is chosen at uniformly random from ${0, 1} l (n) $ and $s$ is chosen at uniform random from ${0, 1} n $

Security of using Stream Cipher for Encrpytion

Consider the construction $Π$ of using $G (k) \oplus m$ as the encryption of $m$

Theorem 3.16. If $G$ is a pseudorandom generator, then $Π$ has indistinguishable encryptions in the presence of an eavesdropper.

Proof idea?

TIP

EAV-secure:

Attacker picks two plaintexts $m 0 , m 1 $ and is given $c = E n c K (m b )$ for random bit $b$ .
Attacker attempts to guess $b$ .
No ability to request additional encryptions (chosen-plaintext attacks)
In fact, no ability to observe any additional encryptions

For more infomation, see here (CS555 lecture 20 spring 2017 PU)open in new window

Properties of Stream Ciphers

Typical stream ciphers are very fast
Widely used, often incorrectly
- Content Scrambling System (uses Linear Feedback Shift Registers incorrectly),
- Wired Equivalent Privacy (uses RC4 incorrectly)
- SSL (uses RC4, SSLv3 has no known major flaw)

Security Properties of Stream Ciphers

Under known plaintext, chosen plaintext, or chosen ciphertext, the adversary knows the key stream (i.e., PRNG(key))
- Security depends on PRNG
- PRNG must be “unpredictable”
Do stream ciphers have perfect secrecy?
How to break a stream cipher in a brute-force way?
If the same key stream is used twice, then easy to break.
- This is a fundamental weakness of stream ciphers; it exists even if the PRNG used in the ciphers is strong

Using Stream Ciphers in Practice

If the same key stream is used twice, then easy to break.
- This is a fundamental weakness of stream ciphers; it exists even if the PRNG used in the ciphers is strong
In practice, one key is used to encrypt many messages
- Example: Wireless communication
- Solution: Use Initial vectors (IV). - $E k e y [M] = [I V, M \oplus P R N G (k e y ∣ ∣ I V)]$
  - IV is sent in clear to receiver;
  - IV needs integrity protection, but not confidentiality protection
  - IV ensures that key streams do not repeat, but does not increase cost of brute-force attacks
  - Without key, knowing IV still cannot decrypt
- Need to ensure that IV never repeats!

Security Against Chosen Plaintext Attacks (CPA security)

Security notions considered so far is for ciphertext-only attacks
Modeling chosen plaintext attacks
- Adversary may choose messages and obtain corresponding ciphertexts adaptively
  - Adaptively means that adversary may look at the ciphertext of the first chosen message, then choose the next message.
- How to model this ability of the adversary?
  - Adversary is given an encryption oracle, which can encrypt messages but does not give out the key

CPA-secure (aka IND-CPA security)

A private-key encryption scheme $Π = (G e n, E n c, D e c)$ has indistinguishable encryption under a chosen-plaintext attack iff for all PPT adversary A, there exists a negligible function negl such that $P r [P r i n K A, Π c p a = 1] \leq 1 / 2 + n e g l (n)$
- No deterministic encryption scheme is CPA-secure. Why? *

Properties of CPA-secure

CPA-secure for multiple messages is equivalent to CPA-secure for a single message
Given a fixed-length encryption scheme that is CPA-secure, we can encrypt messages of arbitrary length by encrypting different parts of messages separately

# Cryptography - One-time Pad, Information Theoretic Security, and Stream Ciphers

# Shannon (Information-Theoretic) Security = Perfect Secrecy

# Explanation of the Definition

# An Equivalent Definition of Perfect Secrecy

# Another equivalent definition

# Example for Information Theoretical Security

# Perfect Secrecy

# The “Bad News” Theorem for Perfect Secrecy

# Stream Ciphers

# Pseudo Random Number Generator

# Randomness and Pseudorandomness

# Distinguisher

# Pseudorandom Generator Definition

# Security of using Stream Cipher for Encrpytion

# Properties of Stream Ciphers

# Security Properties of Stream Ciphers

# Using Stream Ciphers in Practice

# Security Against Chosen Plaintext Attacks (CPA security)

# CPA-secure (aka IND-CPA security)

# Properties of CPA-secure