三重积分
本文主要介绍了三重积分的概念、基本性质以及在不同坐标系下的计算方法。首先，阐述了三重积分的定义，并讨论了其线性性质、区域可加性和积分中值定理等代数性质。接着，介绍了三重积分的换元公式，说明了如何通过坐标变换简化积分计算。
随后，文章分别讲解了在直角坐标系、柱面坐标系和球面坐标系下三重积分的表示形式和计算方法。在每个坐标系中，都详细说明了积分区域的确定方法以及对应的体积元素的变化。通过这些内容，读者可以全面了解三重积分在不同坐标系下的应用，提高对复杂积分问题的处理能力。
（摘要由 OpenAI o1-preview 生成）
三重积分的定义¶
与二重积分类似，三重积分被定义为以下和式的极限：
其中，\(\Omega\) 是三维空间中的某一区域，\(\Delta V_i\) 是 \(\Omega\) 中的某一小体积，\((\xi_i, \eta_i, \zeta_i)\) 是 \(\Delta V_i\) 中的某一点，\(\lambda\) 是 \(\Delta V_i\) 的最大直径。
三重积分的性质¶
三重积分的代数性质¶
三重积分具有和二重积分、单积分相同的代数性质：
(1) 线性性质A：\(\displaystyle \iiint_\Omega k f(x, y, z) \, \mathrm{d}V = k \iiint_\Omega f(x, y, z) \, \mathrm{d}V\)；
(2) 线性性质B：\(\displaystyle \iiint_\Omega [f(x, y, z) \pm g(x, y, z)] \, \mathrm{d}V = \iiint_\Omega f(x, y, z) \, \mathrm{d}V \pm \iiint_\Omega g(x, y, z) \, \mathrm{d}V\)；
(3) 区域可加性：设 \(\Omega\) 可分为有限个互不相交的子区域 \(\Omega_1, \Omega_2, \cdots, \Omega_n\)，则 \(\displaystyle \iiint_\Omega f(x, y, z) \, \mathrm{d}V = \sum_{i=1}^{n} \iiint_{\Omega_i} f(x, y, z) \, \mathrm{d}V\)；
(4) 优势积分：若 \(f(x, y, z) \geq g(x, y, z)\)，则 \(\displaystyle \iiint_\Omega f(x, y, z) \, \mathrm{d}V \geq \iiint_\Omega g(x, y, z) \, \mathrm{d}V\)。
三重积分同样满足积分中值定理，即若 \(f(x, y, z)\) 在 \(\Omega\) 上连续，则至少存在一点 \((\xi, \eta, \zeta) \in \Omega\)，使得
对称性：
(1) 如果积分区域 \(\Omega\) 关于 \(x/y/z\) 轴对称，并且 \(f(x, y, z)\) 是关于 \(x/y/z\) 的奇函数，则有 \(\displaystyle \iiint_\Omega f(x, y, z) \, \mathrm{d}V = 0\)；
(2) 如果积分区域 \(\Omega\) 关于 \(x/y/z\) 轴对称，并且 \(f(x, y, z)\) 是关于 \(x/y/z\) 的偶函数，则有 \(\displaystyle \iiint_\Omega f(x, y, z) \, \mathrm{d}V = 2 \iiint_{\Omega_{1/2}} f(x, y, z) \, \mathrm{d}V\)；
(3) 如果积分区域 \(\Omega\) 中 \(x\) 与 \(y\) 具有等价的地位，则有 \(\displaystyle \iiint_\Omega f(x, y, z) \, \mathrm{d}V = \iiint_{\Omega'} f(y, x, z) \, \mathrm{d}V\)；
(4) 如果积分区域 \(\Omega\) 中 \(x\)，\(y\)，\(z\) 具有等价的地位，则有 \(\displaystyle \iiint_\Omega f(x, y, z) \, \mathrm{d}V = \iiint_{\Omega} f(y, z, x) \, \mathrm{d}V = \iiint_{\Omega} f(z, x, y) \, \mathrm{d}V\)。
三重积分换元法¶
假设用形如 \(\begin{cases} x = x(u, v, w) \\ y = y(u, v, w) \\ z = z(u, v, w) \end{cases}\) （其中 \(x, y, z\) 都是可微函数）的变换，将 \(uvw\) 坐标系中的积分区域 \(\Omega^*\) 一对一地变换为 \(xyz\) 坐标系中的积分区域 \(\Omega\)，则有 $$ \iiint\limits_{\Omega} f(x, y, z) \, \mathrm{d}x \, \mathrm{d}y \, \mathrm{d}z = \iiint\limits_{\Omega^*} f[x(u, v, w), y(u, v, w), z(u, v, w)] \left| \frac{\partial(x, y, z)}{\partial(u, v, w)} \right| \, \mathrm{d}u \, \mathrm{d}v \, \mathrm{d}w $$
其中，\(\displaystyle \frac{\partial(x, y, z)}{\partial(u, v, w)}\) 是雅可比行列式，定义为：
直角坐标系下的三重积分¶
积分区域的确定¶
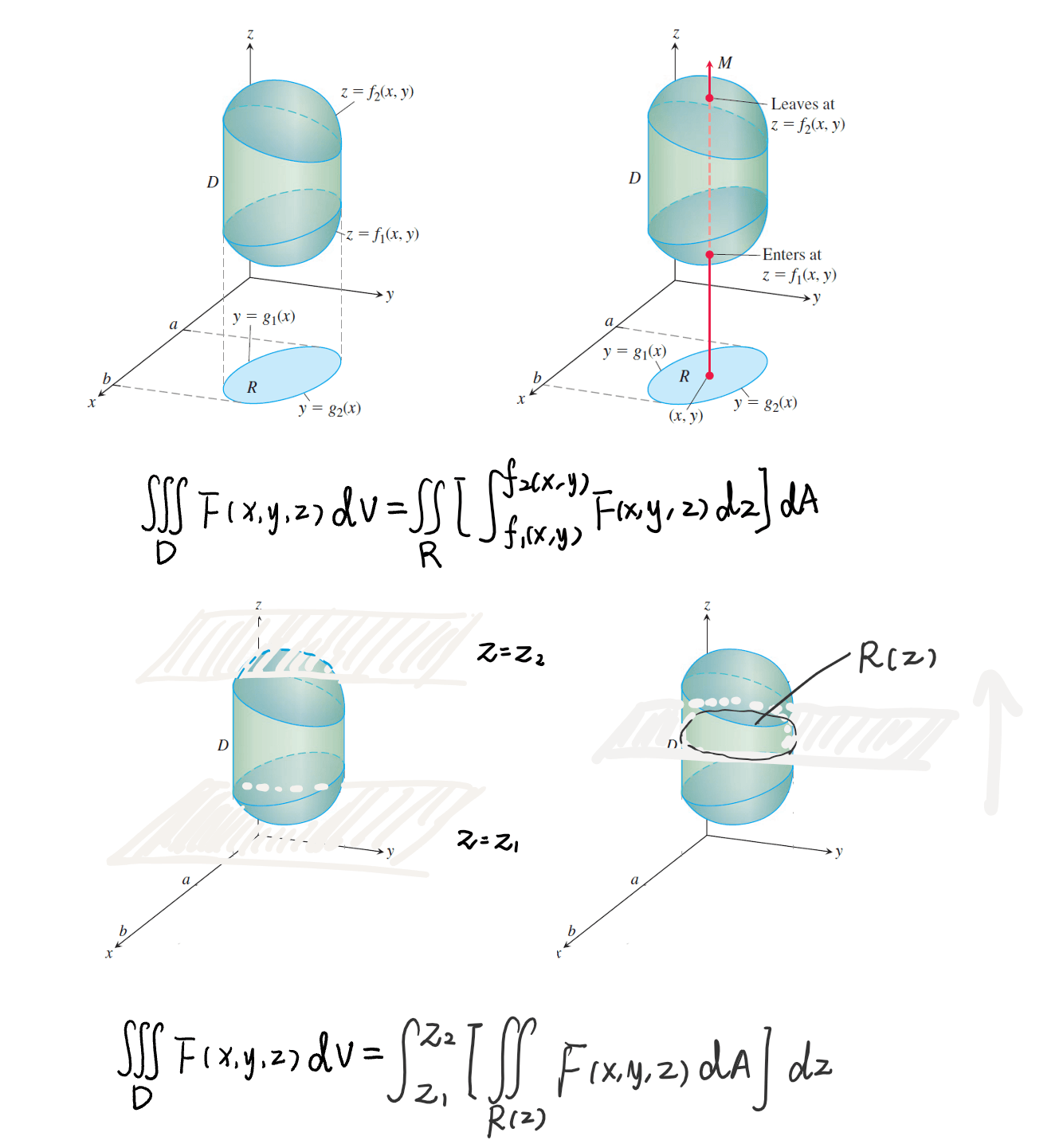
分为两种方法，即先一后二和先二后一。
先一后二：先做对积分变量 \(z\) 的单积分，后在 \(xOy\) 平面某区域（积分区域 \(\Omega\) 在 \(xOy\) 平面上的投影）上做二重积分。
先二后一：先在 \(z = \dots\) 的切面上做二重积分，后从 \(z_{min}\) 到 \(z_{max}\) 做单积分。
这两种方法如图所示1：
柱面坐标系下的三重积分¶
柱面坐标系通过有序三元组 \((r, \theta, z)\) 表示空间中的点 \(P\)，其中 \(r \geq 0\)：
(1) \(r\) 和 \(\theta\) 是点 \(P\) 在 \(xOy\) 平面上的垂直投影的极坐标；
(2) \(z\) 是点 \(P\) 到 \(xOy\) 平面的距离，即直角坐标系中的垂直坐标。
柱面坐标到直角坐标的转换公式为：\(\begin{cases}x = r \cos \theta \\ y = r \sin \theta \\ z = z\end{cases}\)。
依据换元法，有 \(\mathrm{d}V = \mathrm{d}x \, \mathrm{d}y \, \mathrm{d}z = r \, \mathrm{d}r \, \mathrm{d}\theta \, \mathrm{d}z\)，因此转为柱面坐标系下的三重积分公式为：
积分区域的确定¶
一样分为先一后二和先二后一两种方法。
二重积分应当在 \(r\theta\) 平面上的进行计算。这个二重积分的算法见极坐标系下的二重积分。
球面坐标系下的三重积分¶
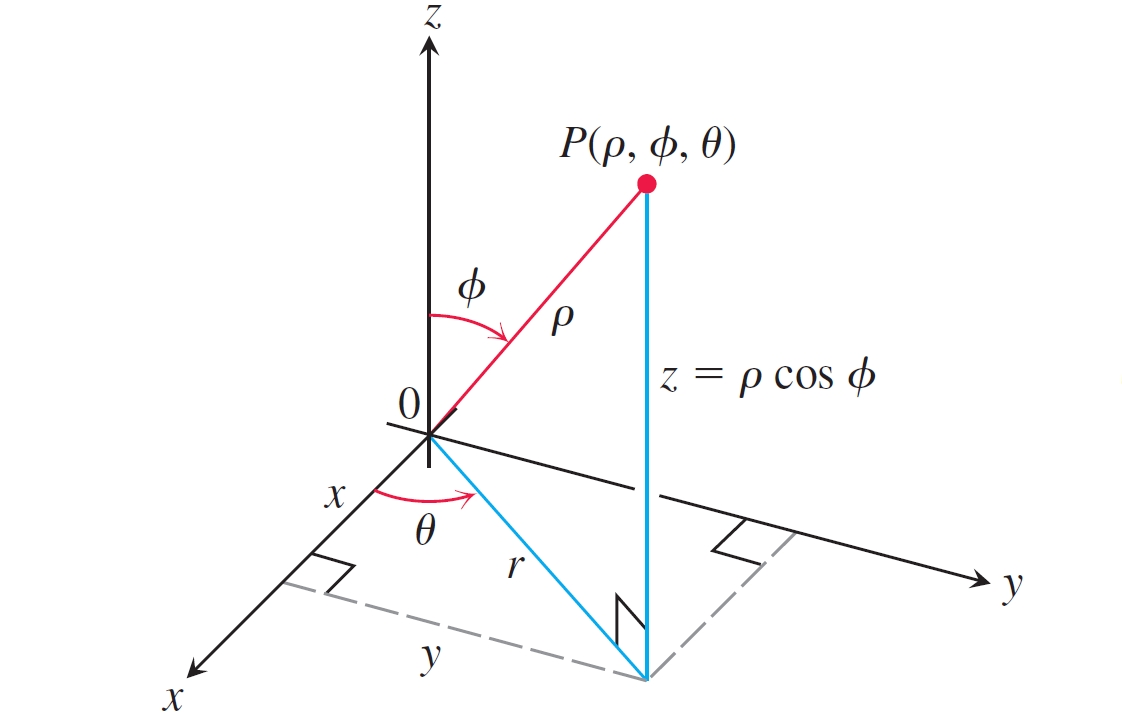
球面坐标系通过有序三元组 \((r, \varphi, \theta)\) 表示空间中的点 \(P\)，其中：
(1) \(r\) 是点 \(P\) 到原点的距离（\(r \geq 0\)）；
(2) \(\varphi\) 是 \(\overrightarrow{OP}\) 与 \(z\) 轴正向之间的夹角（\(0 \leq \varphi \leq \pi\)）；
(3) \(\theta\) 是柱面坐标中的角度。
如图所示2，球面坐标到直角坐标的转换公式为：\(\begin{cases}x = r \sin \varphi \cos \theta \\ y = r \sin \varphi \sin \theta \\ z = r \cos \varphi\end{cases}\)。
依据换元法，有 \(\mathrm{d}V = \mathrm{d}x \, \mathrm{d}y \, \mathrm{d}z = r^2 \sin \varphi \, \mathrm{d}r \, \mathrm{d}\varphi \, \mathrm{d}\theta\)，因此转为球面坐标系下的三重积分公式为：
积分区域的确定¶
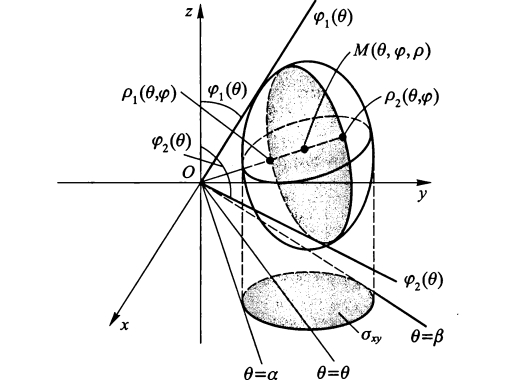
如图所示3，先积 \(\rho\) 后积 \(\varphi\) 后积 \(\theta\)，转化为累次积分。把被积分区域用以下不等式表示：
寻找待定常数和函数 \(\theta_1, \theta_2, \varphi_1, \varphi_2, \rho_1, \rho_2\)，应当依从反过来的顺序，即先确定 \(\theta_1, \theta_2\)，再确定 \(\varphi_1, \varphi_2\)，最后确定 \(\rho_1, \rho_2\)。