空间解析几何
本文概括了空间解析几何的核心内容。首先，介绍了向量的基本运算，如内积（用于计算夹角和投影）和外积（用于求取法向量和面积）。然后，讨论了空间中直线和平面的各种方程形式及其位置关系。接着，介绍了曲线和曲面的表示方法，特别是柱面和旋转曲面，以及曲面的切线和法线的求解方法。最后，简述了常见的二次曲面及其标准方程。本文有助于读者掌握空间解析几何的基本概念和计算技巧。
（摘要由 OpenAI o1-preview 生成）
向量及其基本运算¶
向量的内积（点积、数量积）、外积（叉积、矢量积）¶
三维向量 \(\vec{a} = (a_1, a_2, a_3)\)，\(\vec{b} = (b_1, b_2, b_3)\)。
内积（点积、数量积）：\(\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2 + a_3 b_3 = |\vec{a}| |\vec{b}| \cos \theta\)。
内积将一个向量投影到另一个向量上，得到一个标量。
内积满足交换律：\(\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}\)。
内积满足对加法的分配律：\(\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}\)。
内积满足对数乘的结合律：\((\lambda \vec{a}) \cdot \vec{b} = \lambda (\vec{a} \cdot \vec{b}) = \vec{a} \cdot (\lambda \vec{b})\)。
两个向量的夹角 \(\theta\) 满足 \(\displaystyle \cos \theta = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| |\vec{b}|}\)。
两个向量垂直 \(\Leftrightarrow\) \(\vec{a} \cdot \vec{b} = 0\)。
外积（叉积、矢量积）：\(\vec{a} \times \vec{b} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix}\)。
\(\vec{a} \times \vec{b}\) 是一个垂直于 \(\vec{a}\) 和 \(\vec{b}\) 的向量，且 \(|\vec{a} \times \vec{b}| = |\vec{a}| |\vec{b}| \sin \theta\)。
外积的模长是以 \(\vec{a}\) 和 \(\vec{b}\) 为邻边的平行四边形的面积。
外积不满足交换律：\(\vec{a} \times \vec{b} = - \vec{b} \times \vec{a}\)。
外积满足对加法的分配律：\(\vec{a} \times (\vec{b} + \vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c}\)。
外积满足对数乘的结合律：\((\lambda \vec{a}) \times \vec{b} = \lambda (\vec{a} \times \vec{b}) = \vec{a} \times (\lambda \vec{b})\)。
外积不满足结合律：\(\vec{a} \times (\vec{b} \times \vec{c}) \neq (\vec{a} \times \vec{b}) \times \vec{c}\)。
两个向量平行 \(\Leftrightarrow\) \(\vec{a} \times \vec{b} = 0\)。
向量的数量三重积¶
三维向量 \(\vec{a} = (a_1, a_2, a_3)\)，\(\vec{b} = (b_1, b_2, b_3)\)，\(\vec{c} = (c_1, c_2, c_3)\)。
数量三重积：\((\vec{a}\ \vec{b}\ \vec{c}) = (\vec{a} \times \vec{b}) \cdot \vec{c} = \begin{vmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{vmatrix}\)。
数量三重积的几何意义是，其绝对值 \(|(\vec{a} \times \vec{b}) \cdot \vec{c}|\) 是以 \(\vec{a}\)、\(\vec{b}\)、\(\vec{c}\) 为邻边的平行六面体的体积。
数量三重积交换其中两个向量的位置，值变号：\((\vec{a}\ \vec{b}\ \vec{c}) = - (\vec{b}\ \vec{a}\ \vec{c})\)（等价于行列式中交换两行）。
三个向量共面 \(\Leftrightarrow\) \((\vec{a}\ \vec{b}\ \vec{c}) = 0\)。
空间中的直线和平面¶
直线、平面的方程¶
平面的一般方程：\(Ax + By + Cz + D = 0\)，可以从中得到平面的法向量为 \(\vec{n} = (A, B, C)\)。
平面的点法向式方程：\(A(x - x_0) + B(y - y_0) + C(z - z_0) = 0\)，如果平面过点 \(P_0(x_0, y_0, z_0)\)，且法向量为 \(\vec{n} = (A, B, C)\)。
直线的一般方程：\(\begin{cases} A_1 x + B_1 y + C_1 z + D_1 = 0 \\ A_2 x + B_2 y + C_2 z + D_2 = 0 \end{cases}\)，可以从中得到直线的方向向量为 \(\vec{l} = (A_1, B_1, C_1) \times (A_2, B_2, C_2)\)。
直线的点方向式方程：\(\displaystyle \frac{x - x_0}{l} = \frac{y - y_0}{m} = \frac{z - z_0}{n}\)，其中直线过点 \(P_0(x_0, y_0, z_0)\)，方向向量为 \(\vec{l} = (l, m, n)\)。
直线的参数方程：\(\begin{cases} x = x_0 + l t \\ y = y_0 + m t \\ z = z_0 + n t \end{cases}\)，其中直线过点 \(P_0(x_0, y_0, z_0)\)，方向向量为 \(\vec{l} = (l, m, n)\)。
直线的截距式方程：\(\displaystyle \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\)，其中直线与三个坐标面的交点分别为 \((a, 0, 0)\)、\((0, b, 0)\)、\((0, 0, c)\)。
直线、平面之间的位置关系¶
用直线的方向向量、平面的法向量来判断直线与平面的位置关系。
点、直线、平面之间的距离¶
点到直线的距离：\(\displaystyle d = \frac{|\vec{r} \times \vec{l}|}{|\vec{l}|}\)，其中 \(\vec{r}\) 是点到直线的向量，\(\vec{l}\) 是直线的方向向量。考虑 \(\vec{r}\) 和 \(\vec{l}\) 组成的平行四边形的高。
点到平面的距离：\(\displaystyle d = \frac{|\vec{r} \cdot \vec{n}|}{|\vec{n}|} = \frac{|Ax_0 + By_0 + Cz_0 + D|}{\sqrt{A^2 + B^2 + C^2}}\)，其中 \(\vec{r}\) 是点到平面的向量，\(\vec{n}\) 是平面的法向量。考虑 \(\vec{r}\) 在 \(\vec{n}\) 上的投影长度。展开后得到第二个等号，其中，\(P_0(x_0, y_0, z_0)\) 是点，\(Ax + By + Cz + D = 0\) 是平面。
异面直线的距离：\(\displaystyle d = \frac{|(\vec{l_1} \times \vec{l_2}) \cdot \vec{r}|}{|\vec{l_1} \times \vec{l_2}|}\)，其中 \(\vec{l_1}\) 和 \(\vec{l_2}\) 是两条异面直线的方向向量，\(\vec{r}\) 是两条异面直线上任取两点的连线。考虑由 \(\vec{l_1}\)、\(\vec{l_2}\)、\(\vec{r}\) 构成的平行六面体的高，底是由 \(\vec{l_1}\)、\(\vec{l_2}\) 构成的平行四边形。
直线到平面的距离：隐含的条件是直线与平面平行，此时问题退化为点到平面的距离。
平面到平面的距离：\(\displaystyle d = \frac{|D_1 - D_2|}{\sqrt{A^2 + B^2 + C^2}}\)，其中 \(Ax + By + Cz + D_1 = 0\) 和 \(Ax + By + Cz + D_2 = 0\) 是两个平行平面，考虑以 \(z/x/y\) 轴交平面与两点的连线的长度在法向量 \(\vec{n} = (A, B, C)\) 上的投影。
空间中的曲线和曲面¶
空间内的曲面方程：
以隐函数式给出时：\(F(x, y, z) = 0\)。
有时能转写为显函数：\(z = f(x, y)\)。
空间内的曲线方程：
以参数式给出时：\(\begin{cases} x = x(t) \\ y = y(t) \\ z = z(t) \end{cases}\)。
以一般方程给出时：\(\begin{cases} F(x, y, z) = 0 \\ G(x, y, z) = 0 \end{cases}\)，这实际上是两个空间曲面的交线。
曲面的交线¶
两曲面的交线是两个方程的联立解：曲面 \(F(x, y, z) = 0\) 和 \(G(x, y, z) = 0\) 的交线是 \(\begin{cases} F(x, y, z) = 0 \\ G(x, y, z) = 0 \end{cases}\) 的解。
曲面的交线在 \(xOy\)、\(yOz\)、\(zOx\) 面上的投影：
在 \(xOy\) 面上的投影：联立 \(F(x, y, z) = 0\) 和 \(G(x, y, z) = 0\)，令 \(z\) 项消去，得到 \(H(x, y) = 0\)。再补充 \(z = 0\)，得到 \(\begin{cases} H(x, y) = 0 \\ z = 0\end{cases}\)，即在 \(xOy\) 面上的投影。在其他坐标轴面上的投影同理。
曲线的柱面、旋转曲面¶
柱面：平行于给定直线，并沿曲线（准线）移动的直线（母线）的轨迹。
一般解法：柱面上任意一点 \(P(x, y, z)\) 应当满足：存在曲线上一点 \(Q(x_0, y_0, z_0)\)，使得 \(\overrightarrow{PQ}\) 与母线平行。即 \(\overrightarrow{PQ} = \lambda \vec{l}\)，其中 \(\vec{l}\) 是母线的方向向量。
准线在 \(xOy\) 平面上：\(\begin{cases} f(x, y) = 0 \\ z = z_0 \end{cases}\)，母线平行于 \(z\) 轴的柱面方程：\(f(x, y) = 0\)。
任意的准线 \(\begin{cases} F(x, y, z) = 0 \\ G(x, y, z) = 0 \end{cases}\)，母线平行于 \(z\) 轴的柱面方程：联立后消去 \(z\) 项，得到 \(H(x, y) = 0\)。
旋转曲面：平面曲线绕平面上的一条直线旋转一周所得的曲面。
一般解法：旋转曲面上任意一点 \(P(x, y, z)\) 应当满足：存在曲线上一点 \(Q(x_0, y_0, z_0)\)，使得 \(\overrightarrow{PQ}\) 与旋转轴垂直，并且到旋转轴的距离相等。
\(xOy\) 平面上的曲线 \(\begin{cases} f(x, y) = 0 \\ z = z_0 \end{cases}\)，绕 \(x\) 轴旋转的曲面方程：\(f(x, \pm \sqrt{x^2 + y^2}) = 0\)。
\(xOy\) 平面上的曲线 \(\begin{cases} f(x, y) = 0 \\ z = z_0 \end{cases}\)，绕 \(y\) 轴旋转的曲面方程：\(f(\pm \sqrt{x^2 + y^2}, y) = 0\)。
曲面上一点的法线和切平面¶
曲面上一点的法线方向为 \(\displaystyle \nabla F = \left( \frac{\partial F}{\partial x}, \frac{\partial F}{\partial y}, \frac{\partial F}{\partial z} \right)\)。
已知法线方向，根据点法向式方程，就能够得到切平面的方程。
曲线上一点的切线和法平面¶
当曲线方程由参数式 \(\begin{cases} x = x(t) \\ y = y(t) \\ z = z(t) \end{cases}\) 给出，曲线上一点的切线方向为 \(\displaystyle \frac{\mathrm{d} \vec{r}}{\mathrm{d} t} = \left( \frac{\mathrm{d} x}{\mathrm{d} t}, \frac{\mathrm{d} y}{\mathrm{d} t}, \frac{\mathrm{d} z}{\mathrm{d} t} \right)\)。
当曲线方程由一般方程 \(\begin{cases} F(x, y, z) = 0 \\ G(x, y, z) = 0 \end{cases}\) 给出，曲线上一点的切线方向为 \(\nabla F \times \nabla G\)，即同时垂直于两个曲面的法向量的向量。
已知切线方向，根据点法向式方程，就能够得到法平面的方程。
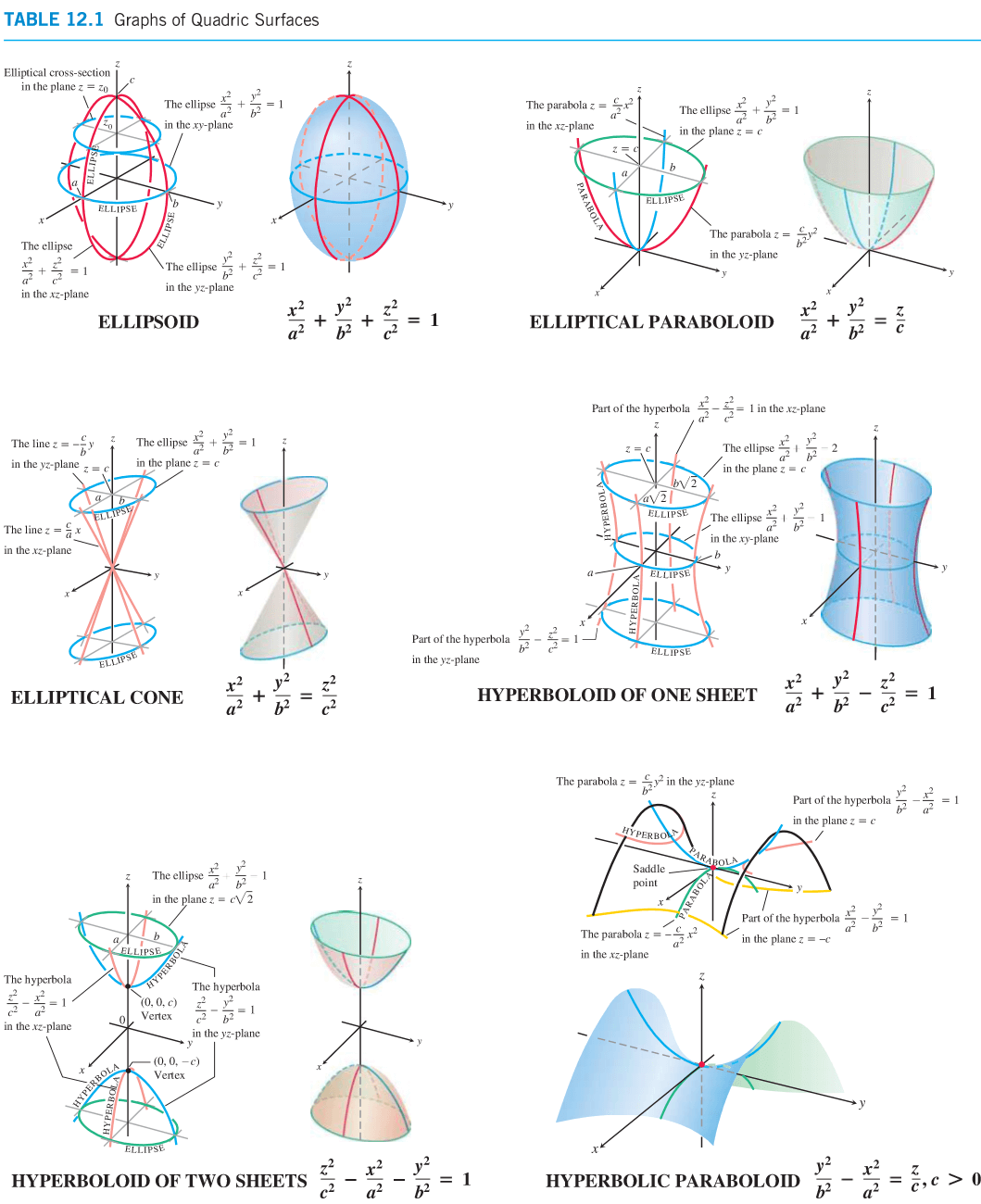
二次曲面¶
常见的二次曲面如下图所示1：
-
Thomas' Calculus 13th Edition, Section 12.6. ↩