曲线积分与曲面积分
本文系统地介绍了曲线积分和曲面积分的基本概念和计算方法。首先讨论了标量场上的第一类曲线积分（线积分）的定义、性质和计算方法。接着探讨了第二类曲线积分（场积分）及其与第一类曲线积分的关系。随后介绍了曲面积分，包括第一类曲面积分（面积分）和第二类曲面积分（通量积分）的定义、性质及计算技巧。文章还阐述了各类积分之间的联系，以及它们在物理学中的实际应用。
（摘要由 Claude 3.5 Sonnet 生成）
标量场上的线积分（第一类曲线积分）¶
第一类曲线积分的定义¶
设 \(C\) 是平面上以 \(A, B\) 为端点的一条光滑曲线。\(f(x, y)\) 是定义在曲线 \(C\) 上的有界函数。
在曲线上任意取点 \(A = M_0, M_1, M_2, \cdots, M_n = B\)，将曲线 \(C\)分成 \(n\) 段，记作 \(\Delta s_1, \Delta s_2, \cdots, \Delta s_n\)。
设 \((\xi_i, \eta_i)\) 是 \(\Delta s_i\) 上的任意一点，\(f(\xi_i, \eta_i)\) 是 \((\xi_i, \eta_i)\) 处的函数值。
记 \(\lambda = \max \{ \Delta s_1, \Delta s_2, \cdots, \Delta s_n \}\)，则以下的和式的极限称为函数 \(f(x, y)\) 沿曲线 \(C\) 从 \(A\) 到 \(B\) 的第一类曲线积分（如果极限存在）：
第一类曲线积分的代数性质¶
第一类曲线积分具有和单积分相同的代数性质，即线性性、路径可加性和优势积分性质。第一类曲线积分也满足积分中值定理。
此外，第一类曲线积分不强调曲线的方向，即 \(\displaystyle \int_C f(x, y) ds = \int_{-C} f(x, y) ds\)。
当积分路径由参数方程给出，直接计算第一类曲线积分的方法¶
当曲线 \(C\) 由参数方程 \(\begin{cases} x = \varphi(t) \\ y = \psi(t) \end{cases}\) 给出时：
可以证明，弧长的增量 \(\Delta s = \sqrt{(\varphi'(t))^2 + (\psi'(t))^2} \Delta t + o(\Delta t)\)。
从而 \(ds = \sqrt{(\varphi'(t))^2 + (\psi'(t))^2} dt\)。
那么：
\(\displaystyle \int_C f(x, y) ds = \int_{t_1}^{t_2} f \Big(\varphi(t), \psi(t) \Big) \sqrt{(\varphi'(t))^2 + (\psi'(t))^2} dt\)。
其中，\(t_1, t_2\) 是参数 \(t\) 的取值范围，从小到大。
向量场上的线积分（第二类曲线积分）¶
第二类曲线积分的定义¶
设 \(C\) 是平面上以 \(A, B\) 为端点的一条光滑曲线，并指定从 \(A\) 到 \(B\) 的曲线方向。
在曲线 \(C\) 上取一点 \(M(x, y)\)。
设 \(M\) 处的向量场为 \(\mathbf{F}(M) = \begin{bmatrix} P(x, y) \\ Q(x, y) \end{bmatrix}\)。
设 \(\mathbf{e}_c(M)\) 是曲线 \(C\) 在点 \(M\) 处的单位切向量，即 \(\mathbf{e}_c(M) = \begin{bmatrix} \cos \alpha \\ \cos \beta \end{bmatrix}\)，其中 \(\alpha\)、\(\beta\) 是曲线 \(C\) 在点 \(M\) 处的切线与 \(x\) 轴、\(y\) 轴正方向的夹角。
那么向量场 \(\mathbf{F}(M)\) 沿曲线 \(C\) 从 \(A\) 到 \(B\) 的第二类曲线积分，被定义为以下的第一类曲线积分：
将 \(\mathbf{e}_c(M) ds\) 记作有向线元 \(d\mathbf{s}\)，第二类曲线积分可以写成 \(\displaystyle \int_C \mathbf{F} \cdot d\mathbf{s}\)。
第二类曲线积分的代数性质¶
第一类曲线积分具有和单积分相同的代数性质，即线性性、路径可加性和优势积分性质。第二类曲线积分也满足积分中值定理。
第二类曲线积分强调曲线的方向，即 \(\displaystyle \int_C \mathbf{F} \cdot d\mathbf{s} = -\int_{-C} \mathbf{F} \cdot d\mathbf{s}\)。
当积分路径由参数方程给出，直接计算第二类曲线积分的方法¶
设曲线 \(C\) 由参数方程 \(\begin{cases} x = \varphi(t) \\ y = \psi(t) \end{cases}\) 给出，曲线两端点分别为 \(A(\varphi(t_1), \psi(t_1))\)、\(B(\varphi(t_2), \psi(t_2))\)，那么：
Note
证明：分别证明 \(\displaystyle \int_C P dx = \int_{t_1}^{t_2} P \Big(\varphi(t), \psi(t) \Big) \varphi'(t) dt\) 和 \(\displaystyle \int_C Q dy = \int_{t_1}^{t_2} Q \Big(\varphi(t), \psi(t) \Big) \psi'(t) dt\)。使用一元定积分的定义和拉格朗日中值定理。需要对 \(t_1, t_2\) 大小关系进行讨论，但会得到相同的结果。具体证明此处从略。
格林公式¶
设闭区域 \(D\) 由分段光滑的简单曲线 \(C\) 围成，函数 \(P(x, y)\) 和 \(Q(x, y)\) 在 \(D\) 上具有一阶连续偏导数，则有：
其中，\(C^+\) 是 \(D\) 的正向边界曲线。
正向边界是指，当观察者沿着曲线 \(C\) 的方向，区域 \(D\) 始终在左侧。格林公式的情况是，曲线积分取曲线 \(C\) 逆时针方向。
光滑曲线是指，曲线 \(C\) 在其上的每一点都有切线，并且切线方向连续变化。即 \(x'(t)\)、\(y'(t)\) 存在且连续，并且不同时为 \(0\)。
分段光滑曲线是指，曲线 \(C\) 由有限条光滑曲线组成（不要求连接处的切线方向一致）。
简单曲线是指，曲线 \(C\) 除了端点处，不与自身相交。
平面上第二类曲线积分的路径无关性¶
在单连通区域 \(D\) 上，可以证明以下四个命题等价：
- 向量场 \(\mathbf{F} = \begin{bmatrix} P(x, y) \\ Q(x, y) \end{bmatrix}\) 是保守场，即 \(\displaystyle P dx + Q dy\) 是某个函数的全微分；
- \(\begin{vmatrix} \displaystyle \frac{\partial}{\partial x} & \displaystyle \frac{\partial}{\partial y} \\ P & Q \end{vmatrix} = 0\)，即 \(\displaystyle \frac{\partial Q}{\partial x} = \frac{\partial P}{\partial y}\)；
- 沿 \(D\) 内任意逐段光滑闭曲线 \(C\)，有 \(\displaystyle \oint_C \mathbf{F} \cdot d\mathbf{s} = 0\)；
- 沿 \(D\) 内任意逐段光滑的曲线 \(L_{AB}\)，有 \(\displaystyle \int_{L_{AB}} \mathbf{F} \cdot d\mathbf{s}\) 与路径无关，只与起点 \(A\) 和终点 \(B\) 有关。
提出线积分的基本定理：如果向量场 \(\mathbf{F} = \begin{bmatrix} P(x, y) \\ Q(x, y) \end{bmatrix}\) 是保守场，即存在标量场 \(f(x, y)\)，使得 \(\nabla f = \mathbf{F}\)，设曲线 \(C\) 由点 \(A\) 到点 \(B\)，那么：
空间中第二类曲线积分的路径无关性¶
有关平面上第二类曲线积分的路径无关性的结论，可以直接推广到空间中的情况。
在单连通区域 \(\Omega\) 上，以下四个命题等价：
- 向量场 \(\mathbf{F} = \begin{bmatrix} P(x, y, z) \\ Q(x, y, z) \\ R(x, y, z) \end{bmatrix}\) 是保守场，即存在标量场 \(f(x, y, z)\)，使得 \(\nabla f = \mathbf{F}\)；
- 向量场 \(\mathbf{F} = \begin{bmatrix} P(x, y, z) \\ Q(x, y, z) \\ R(x, y, z) \end{bmatrix}\) 的旋度为零，即 \(\nabla \times \mathbf{F} = \mathbf{0}\)；
- 沿 \(\Omega\) 内沿任意逐段光滑闭曲线 \(C\)，有 \(\displaystyle \oint_C \mathbf{F} \cdot d\mathbf{s} = 0\)；
- 沿 \(\Omega\) 内任意逐段光滑的曲线 \(L_{AB}\)，有 \(\displaystyle \int_{L_{AB}} \mathbf{F} \cdot d\mathbf{s}\) 与路径无关，只与起点 \(A\) 和终点 \(B\) 有关。
应用：使用格林公式计算平面参数曲线围成的面积¶
由格林公式 \(\displaystyle \iint_D \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) dA = \oint_C P dx + Q dy\)，只需要构造一组合适的 \(P\)、\(Q\)，使得 \(\displaystyle \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = 1\)，即可计算曲线围成的面积。
我们选取 \(\begin{cases} P = 0 \\ Q = x \end{cases}\)，则 \(\displaystyle \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = 1\)，即满足条件。
或者选取 \(\begin{cases} P = -y \\ Q = 0 \end{cases}\)，同样满足条件。
从而，\(\displaystyle A = \oint_C x dy = -\oint_C y dx = \frac{1}{2} \oint_C (x dy - y dx)\)。
具体选取何种形式取决于计算的方便程度。
标量场上的面积分（第一类曲面积分）¶
设 \(S\) 是空间内的一块光滑曲面。而 \(f(x, y, z)\) 是定义在曲面 \(S\) 上的有界函数。
用曲线网将 \(S\) 任意分为 \(n\) 个小面元，记作 \(\Delta S_1, \Delta S_2, \cdots, \Delta S_n\)。
设 \((\xi_i, \eta_i, \zeta_i)\) 是 \(\Delta S_i\) 上的任意一点，\(f(\xi_i, \eta_i, \zeta_i)\) 是 \((\xi_i, \eta_i, \zeta_i)\) 处的函数值。
记 \(\lambda = \max \{ \Delta S_1, \Delta S_2, \cdots, \Delta S_n \}\)，则以下的和式的极限称为函数 \(f(x, y, z)\) 沿曲面 \(S\) 的第一类曲面积分（如果极限存在）：
第一类曲面积分的代数性质¶
第一类曲面积分具有和单积分相同的代数性质，即线性性、积分区域可加性和优势积分性质。第一类曲面积分也满足积分中值定理。
第一类曲面积分不强调曲面的定向，即 \(\displaystyle \int_S f(x, y, z) dS = \int_{-S} f(x, y, z) dS\)。
如果积分曲面由直角坐标方程给出，直接计算第一类曲面积分的方法¶
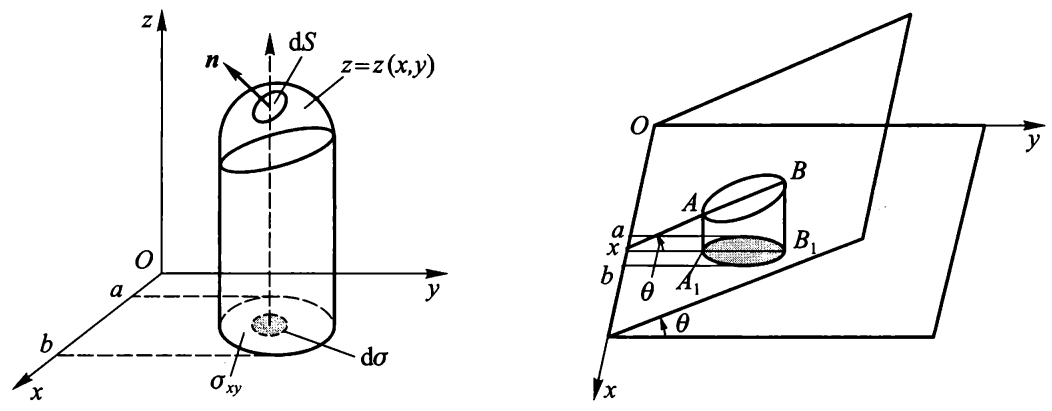
设曲面 \(S\) 由方程 \(F(x, y, z) = 0\) 给出，我们尝试将曲面投影到 \(xOy\) 平面上，对曲面积分进行计算。
如图所示1，有 \(d\sigma = |\cos \gamma| dS\)。
而曲面上任意一点 \((x, y, z)\) 处，有 \(\displaystyle \cos \gamma = \frac{\mathbf{n} \cdot \mathbf{k}}{|\mathbf{n}| |\mathbf{k}|}\)。
而 \(\mathbf{n} = \nabla F = \begin{bmatrix} F'_x \\ F'_y \\ F'_z \end{bmatrix}\)，\(\mathbf{k} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}\)，从而：
从而：
特别地，如果曲面 \(S\) 由 \(z = z(x, y)\) 给出，那么 \(F'_z = 1\)，从而：
向量场上的面积分（第二类曲面积分）¶
第二类曲面积分的定义¶
设 \(S\) 是空间内的一块光滑曲面，并指定曲面 \(S\) 的定向。
在曲面 \(S\) 上取一点 \(M(x, y, z)\)。
设 \(M\) 处的向量场为 \(\mathbf{F}(M) = \begin{bmatrix} P(x, y, z) \\ Q(x, y, z) \\ R(x, y, z) \end{bmatrix}\)。
设 \(\mathbf{n}_c(M)\) 是曲面 \(S\) 在点 \(M\) 处的单位法向量，即 \(\mathbf{n}_c(M) = \begin{bmatrix} \cos \alpha \\ \cos \beta \\ \cos \gamma \end{bmatrix}\)，其中 \(\alpha\)、\(\beta\)、\(\gamma\) 是曲面 \(S\) 在点 \(M\) 处的法线与 \(x\) 轴、\(y\) 轴、\(z\) 轴正方向的夹角。
那么向量场 \(\mathbf{F}(M)\) 对定向曲面 \(S\) 的第二类曲面积分，被定义为以下的第一类曲面积分：
将 \(\mathbf{n}_c(M) dS\) 记作有向面元 \(d\mathbf{S}\)，第二类曲面积分可以写成 \(\displaystyle \iint_S \mathbf{F} \cdot d\mathbf{S}\)。
\(d\mathbf{S}\) 在三个坐标面上的投影为 \(\begin{cases}\mathbf{i} \cdot d\mathbf{S} = \cos \alpha dS = dy dz \\ \mathbf{j} \cdot d\mathbf{S} = \cos \beta dS = dz dx \\ \mathbf{k} \cdot d\mathbf{S} = \cos \gamma dS = dx dy \end{cases}\)。
采用这里的 \(dy dz\)、\(dz dx\)、\(dx dy\) 作为面积微元的记法时，需要注意此处是考虑方向的，即 \(dz dx = -dx dy\)。
第二类曲面积分的代数性质¶
第二类曲面积分具有和单积分相同的代数性质，即线性性、积分区域可加性和优势积分性质。第二类曲面积分也满足积分中值定理。
第二类曲面积分强调曲面的方向，即 \(\displaystyle \iint_S \mathbf{F} \cdot d\mathbf{S} = -\iint_{-S} \mathbf{F} \cdot d\mathbf{S}\)。
如果积分曲面由直角坐标方程给出，直接计算第二类曲面积分的方法¶
根据定义
我们考虑其中一项 \(\displaystyle \iint_S R dx dy\) 的计算。
将曲面 \(S\) 投影到 \(xOy\) 平面上，得到投影区域 \(D_{xy}\)。
在这个积分区域 \(D\) 上的面积元 \(d\sigma\) 与 \(dS\) 之间的关系是 \(d\sigma = dS |\cos \gamma|\)。
从而：
其中，\(\pm\) 取决于曲面定向 \(\mathbf{n}\) 在 \(z\) 轴正方向的投影的方向，若投影为正方向，则取正号；否则取负号。
高斯公式¶
设空间区域 \(V\) 由分片光滑的闭曲面 \(S\) 围成，函数 \(P(x, y, z)\)、\(Q(x, y, z)\)、\(R(x, y, z)\) 在 \(V\) 上具有一阶连续偏导数，则有：
其中，\(S^+\) 是 \(V\) 的外侧曲面。
定义 \(\displaystyle \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z}\) 为 \(\mathbf{F} = \begin{bmatrix} P(x, y, z) \\ Q(x, y, z) \\ R(x, y, z) \end{bmatrix}\) 的散度，记作 \(\nabla \cdot \mathbf{F}\)，那么高斯公式可以写成：
散度的物理意义是，某一点的场强的流出量与流入量之差。
斯托克斯公式¶
设分片光滑的闭曲面 \(S\) 的边界曲线 \(C\) 为分段光滑曲线，函数 \(P(x, y, z)\)、\(Q(x, y, z)\)、\(R(x, y, z)\) 在 \(V\) 上具有一阶连续偏导数，则有：
其中，\(S\) 的定向与曲线 \(C\) 的方向满足右手法则。
其行列式形式为：
定义 \(\begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ \displaystyle \frac{\partial}{\partial x} & \displaystyle \frac{\partial}{\partial y} & \displaystyle \frac{\partial}{\partial z} \\ P & Q & R \end{vmatrix}\) 为 \(\mathbf{F} = \begin{bmatrix} P(x, y, z) \\ Q(x, y, z) \\ R(x, y, z) \end{bmatrix}\) 的旋度，记作 \(\nabla \times \mathbf{F}\)，那么斯托克斯公式可以写成：
-
苏德矿 《微积分（下）》，第 10.4.2 节，图 9.48，图 9.49 ↩