使用积分求解几何量

高等数学之用积分求解几何量。省流：

几何量	方法	说明
面积	\(\displaystyle \iint_D 1\,dA\)	区域 \(D\) 的二重积分
弧长	\(\displaystyle \int_L 1\,ds\)	曲线 \(L\) 的第一类曲线积分
体积（绕 \(x\) 轴）	\(\displaystyle V = \int_a^b \pi [f(x)]^2\,dx\)	\(y=f(x)\) 绕 \(x\) 轴旋转
体积（绕 \(y\) 轴）	\(\displaystyle V = \int_a^b 2\pi x f(x)\,dx\)	\(y=f(x)\) 绕 \(y\) 轴旋转
侧面积（绕 \(x\) 轴）	\(\displaystyle S = \int_L 2\pi y\,ds\)	曲线绕 \(x\) 轴旋转
形心	\(\displaystyle \left( \frac{\iint_D x\,dA}{\iint_D 1\,dA},\ \frac{\iint_D y\,dA}{\iint_D 1\,dA} \right)\)	平面区域 \(D\) 的形心
弧长微分	\(\displaystyle ds = \sqrt{\left[\varphi'(t)\right]^2 + \left[\psi'(t)\right]^2}dt\)	参数方程表示
	\(\displaystyle ds = \sqrt{1 + \left[f'(x)\right]^2}dx\)	\(y = f(x)\) 表示
	\(\displaystyle ds = \sqrt{\left[r(\theta)\right]^2 + \left[r'(\theta)\right]^2}d\theta\)	极坐标方程表示

平面图形的面积、周长

平面曲线所围成的面积

等价于计算在区域上的二重积分 \(\displaystyle \iint_D 1 dA\)。

根据情况决定积分顺序计算二重积分即可。

平面曲线的弧长

假设平面曲线由参数方程 \(\begin{cases} x = \varphi(t) \\ y = \psi(t) \end{cases}\) 给出：

问题等价于计算第一类曲线积分 \(\displaystyle \int_L 1 ds\)。

弧长的微分：\(\displaystyle ds = \sqrt{(dx)^2 + (dy)^2}\)。

当曲线由参数方程 \(\begin{cases} x = \varphi(t) \\ y = \psi(t) \end{cases}\) 给出时，弧长的微分 \(\displaystyle ds = \sqrt{\left[\varphi'(t)\right]^2 + \left[\psi'(t)\right]^2}dt\)。

当曲线由 \(y = f(x)\) 给出时，弧长的微分 \(\displaystyle ds = \sqrt{1 + \left[f'(x)\right]^2}dx\)。

当曲线由 \(r = r(\theta)\) 给出时，弧长的微分 \(\displaystyle ds = \sqrt{\left[r(\theta)\right]^2 + \left[r'(\theta)\right]^2}d\theta\)。这个式子通过代入 \(\begin{cases} x = r(\theta) \cos \theta \\ y = r(\theta) \sin \theta \end{cases}\) 到弧长微分公式中得到。

对弧长微分的推导

曲线弧长的定义：设 $A$、$B$ 为平面曲线 $\Gamma$ 的两端点，在 $\Gamma$ 上按顺序任意取点 $M_0 = A, M_1, M_2, \cdots, M_n = B$，连接 $M_0, M_1, M_2, \cdots, M_n$，得到折线 $M_0M_1M_2\cdots M_n$。 记 $\displaystyle \lambda = \max_{1 \leq i \leq n} \overline{M_{i-1} M_i}$，$\displaystyle s = \sum_{i=1}^n \overline{M_{i-1} M_i}$，如果 $\displaystyle \lim_{\lambda \to 0} s$ 存在，并且与 $M_i$ 的选取无关，则称此极限为曲线 $\Gamma$ 的弧长。 计算当参数 $t$ 增加 $\Delta t$ 时，曲线上的两点之间的距离 $\Delta s$。 当 $\Delta t \to 0$，$\Delta s \approx \sqrt{(\Delta x)^2 + (\Delta y)^2}$（来自曲线弧长的定义）。 而 $$ \begin{array}{rl} \displaystyle \sqrt{(\Delta x)^2 + (\Delta y)^2} &= \displaystyle \sqrt{(\varphi(t + \Delta t) - \varphi(t))^2 + (\psi(t + \Delta t) - \psi(t))^2} \\ &= \displaystyle \sqrt{(\varphi'(\xi) \Delta t)^2 + (\psi'(\eta) \Delta t)^2} \qquad (\xi, \eta \in (t, t + \Delta t)) \\ &= \displaystyle \sqrt{(\varphi'(\xi))^2 + (\psi'(\eta))^2} \Delta t \\ &= \displaystyle \sqrt{(\varphi'(t))^2 + (\psi'(t))^2} \Delta t + \Big(-\sqrt{(\varphi'(t))^2 + (\psi'(t))^2} + \sqrt{(\varphi'(\xi))^2 + (\psi'(\eta))^2}\Big)\Delta t \end{array} $$ 现证明 $\Big(-\sqrt{(\varphi'(t))^2 + (\psi'(t))^2} + \sqrt{(\varphi'(\xi))^2 + (\psi'(\eta))^2}\Big)\Delta t$ 是 $\omicron(\Delta t)$： $$ \begin{array}{rl} & \displaystyle \lim_{\Delta t \to 0} \frac{\Big(-\sqrt{(\varphi'(t))^2 + (\psi'(t))^2} + \sqrt{(\varphi'(\xi))^2 + (\psi'(\eta))^2}\Big)\Delta t}{\Delta t} \\ =& \displaystyle \lim_{\Delta t \to 0} \Big( - \sqrt{(\varphi'(t))^2 + (\psi'(t))^2} + \sqrt{(\varphi'(\xi))^2 + (\psi'(\eta))^2}\Big) \\ =& \displaystyle -\lim_{\Delta t \to 0} \sqrt{(\varphi'(t))^2 + (\psi'(t))^2} + \lim_{\Delta t \to 0} \sqrt{(\varphi'(\xi))^2 + (\psi'(\eta))^2} \\ =& \displaystyle -\sqrt{(\varphi'(t))^2 + (\psi'(t))^2} + \sqrt{(\varphi'(t))^2 + (\psi'(t))^2} \\ =& \displaystyle 0 \end{array} $$ 从而 $\displaystyle \sqrt{(\Delta x)^2 + (\Delta y)^2} = \sqrt{(\varphi'(t))^2 + (\psi'(t))^2} \Delta t + \omicron(\Delta t)$。也即 $\displaystyle \sqrt{(\Delta x)^2 + (\Delta y)^2}$ 的微分形式为 $\displaystyle \sqrt{(\varphi'(t))^2 + (\psi'(t))^2} dt$。 从而 $\displaystyle ds = \sqrt{(\varphi'(t))^2 + (\psi'(t))^2} dt$。

旋转体的体积、侧面积

y = f(x) 绕 x 轴旋转一周所得的体积

等价于计算在区域上的三重积分 \(\displaystyle \iiint_V 1 dV\)。先对横截面积分再对高度积分。

\[ \begin{array}{rl} \displaystyle V &= \displaystyle \iiint_V 1 dV \\ &= \displaystyle \int_a^b \iint_{D_x} 1 dA dx \\ &= \displaystyle \int_a^b \pi f(x)^2 dx \end{array} \]

当曲线由极坐标方程 \(r = r(\theta)\) 给出时，通过计算 \(\displaystyle \int_a^b \pi y^2 dx\) 可以得到体积。其中，\(y = r(\theta) \sin \theta\)，\(dx = d\big(r(\theta) \cos \theta\big)\)。

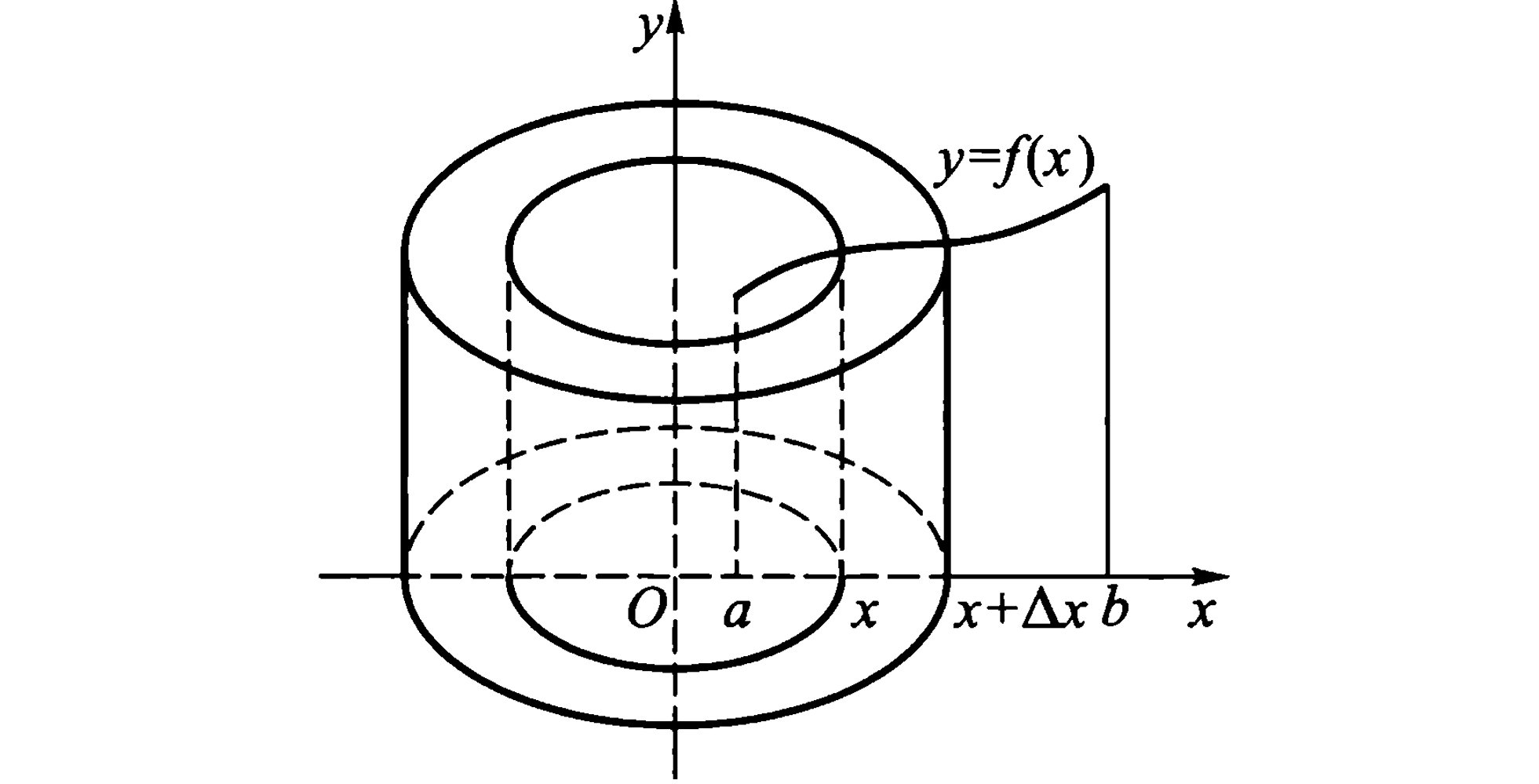
y = f(x) 绕 y 轴旋转一周所得的体积

求解如图所示的区域绕 \(y\) 轴旋转一周所得体积。

有两种方法：

通过微元法可以得到 \(\displaystyle dV = \pi [(x + dx)^2 - \pi x^2]y = 2\pi xy dx\)，从而

\[ V = \int_{a}^{b} 2\pi x f(x) dx \]

参照绕 \(x\) 轴旋转一周所得体积的方式（用直线 \(y = f(a)\) 将区域分成两个部分进行计算），可以得到：

\[ V = \pi (b^2 - a^2) f(a) + \int_{f(a)}^{f(b)} \pi (b^2 - x^2) dy \]

这两种方法给出的结果可以通过分部积分法互相转换。在第二种方法中，令 \(y = f(x)\)，从而

\[ \begin{array}{rl} \displaystyle V &= \displaystyle \pi (b^2 - a^2) f(a) + [f(b) - f(a)] \pi b^2 - \int_{a}^{b} \pi x^2 df(x) \\ &= \displaystyle - \pi a^2 f(a) + \pi b^2 f(b) - \pi x^2 f(x) \Big|_{a}^{b} + 2 \int_{a}^{b} \pi x f(x) dx \\ &= \displaystyle \int_{a}^{b} 2\pi x f(x) dx \end{array} \]

由参数方程给出的曲线绕 x 轴旋转一周所得的侧面积

假设平面曲线由参数方程 \(\begin{cases} x = \varphi(t) \\ y = \psi(t) \end{cases}\) 给出。求该曲线绕 \(x\) 轴旋转一周所得立体的表面积：

使用第二类曲线积分然后使用高斯定理进行计算不是一个好的选择。

使用微元法，可以得到： $$ \begin{array}{rl} \displaystyle S &= \displaystyle \int_L 2\pi y ds \ &= \displaystyle \int_{t1}^{t2} 2\pi \psi(t) \sqrt{(\varphi'(t))^2 + (\psi'(t))^2} dt \end{array} $$

直观解释：对每一小段曲线 \(ds\) 计算其绕 \(x\) 轴旋转一周所得周长，然后将所有小段曲线的周长累加起来。

对表面积微元的推导

使用微元法，计算 $[t, t + \Delta t]$ 小段上的曲线绕 $x$ 轴旋转一周所得的小圆台的侧面积 $\Delta S$。 与计算平面曲线的长度时一致，当 $\Delta t \to 0$ 时，可以将原本是小段曲线的圆台母线 $\Delta s$ 近似为长为 $\sqrt{(\Delta x)^2 + (\Delta y)^2}$ 的直线，从而侧面积 $$ \begin{array}{rl} \displaystyle \Delta S &\approx \displaystyle \pi (R + r) l \\ &= \displaystyle \pi (2y + \Delta y) \sqrt{(\Delta x)^2 + (\Delta y)^2} \\ &= \pi (2y + \Delta y) \Big( \sqrt{(\varphi'(t))^2 + (\psi'(t))^2} \Delta t + \omicron(\Delta t) \Big) \\ &= 2 \pi y \sqrt{(\varphi'(t))^2 + (\psi'(t))^2} \Delta t + \pi \Delta y \sqrt{(\varphi'(t))^2 + (\psi'(t))^2} \Delta t + \omicron(\Delta t) \\ \end{array} $$ 又 $$ \begin{array}{rl} &\displaystyle \lim_{\Delta t \to 0} \frac{\Delta y \sqrt{(\varphi'(t))^2 + (\psi'(t))^2} \Delta t}{\Delta t} \\ =& \displaystyle \lim_{\Delta t \to 0} \psi'(\eta) \sqrt{(\varphi'(t))^2 + (\psi'(t))^2}\Delta t \qquad (\eta \in (t, t + \Delta t)) \\ =& \displaystyle 0 \end{array} $$ 从而，$\displaystyle \Delta S = 2\pi y \sqrt{(\varphi'(t))^2 + (\psi'(t))^2} \Delta t + \omicron(\Delta t)$，即 $$ dS = 2\pi y \sqrt{(\varphi'(t))^2 + (\psi'(t))^2} dt = 2\pi y ds $$

物理量

平面区域的形心

平面区域 \(D\) 的形心：\(\left( \displaystyle \frac{\displaystyle \iint_D x\,dA}{\displaystyle \iint_D 1\,dA}, \displaystyle \frac{\displaystyle \iint_D y\,dA}{\displaystyle \iint_D 1\,dA} \right)\)

以 \(\bar{x}\) 为例，形心的 \(x\) 坐标的直观意义为 平面区域 \(D\) 上所有点的横坐标之平均值。参考一元函数的平均值 \(\overline{f(x)} = \displaystyle \frac{\displaystyle \int_a^b f(x) dx}{\displaystyle \int_a^b 1 dx}\)，二元函数 \(f(x,y) = x\) 在区域 D 上的平均值为 \(\overline{x} = \displaystyle \frac{\displaystyle \iint_D x\,dA}{\displaystyle \iint_D 1\,dA}\)。

质量非均匀分布区域的质心

质量均匀分布的平面区域，其质心等于形心。而对非均匀分布的区域，假设密度分布函数为 \(\rho(x, y)\)，其质心为 \(\left( \displaystyle \frac{\displaystyle \iint_D \rho(x, y) \cdot x\,dA}{\displaystyle \iint_D \rho(x, y)\,dA}, \displaystyle \frac{\displaystyle \iint_D \rho(x, y) \cdot y\,dA}{\displaystyle \iint_D \rho(x, y)\,dA} \right)\)

求静压力、做功问题

大部分问题都可以通过取某个平面作为微元，计算来自微元的静压力或对微元所做的功，然后对高度进行积分得到。