二重积分
本文详细介绍了二重积分的基本概念和计算方法。首先定义了二重积分的黎曼和，解释了如何通过将区域分割成小矩形并求和来计算二重积分。接着，讨论了二重积分的基本性质，包括线性性、可加性和优势积分等。随后，介绍了富比尼定理，说明了如何将二重积分转化为累次积分，并给出了在直角坐标系和极坐标系下计算二重积分的方法。文章还探讨了二重积分的一般换元法，介绍了通过坐标变换简化积分计算的技巧。最后，通过多个例题展示了如何应用对称性、换元法和曲线积分等方法来简化和计算复杂的二重积分。通过本文的学习，读者可以全面掌握二重积分的理论基础和计算技巧。
（摘要由 OpenAI GPT 4o 生成）
二重积分的黎曼和
二重积分的定义
考虑定义在有界闭区域 \(D\) 上的函数 \(f(x, y)\)，将 \(D\) 平行于坐标轴地分割成 \(k\) 个小矩形 \(D_{ij}\)，其中 \(i = 1, 2, \cdots, n\)，\(j = 1, 2, \cdots, m\)。设 \(D_{ij}\) 的面积为 \(\Delta A_{ij}\)，取 \(D_{ij}\) 中任意一点 \((\xi_{ij}, \eta_{ij})\)，将 \(f(\xi_{ij}, \eta_{ij})\) 与 \(\Delta A_{ij}\) 的乘积求和：
\[
S = \sum_{i=1}^n \sum_{j=1}^m f(\xi_{ij}, \eta_{ij}) \Delta A_{ij}
\]
对于 \(S\)，根据划分的不同以及 \(f(\xi_{ij}, \eta_{ij})\) 的不同选取方法，可能得到不同的值。
定义划分的范数 \(||P||\) 为 \(D\) 中所有小矩形的最大直径，如果当 \(||P|| \to 0\) 时，\(S\) 的极限存在，且无论做什么选择都是都给出同一个极限值，那么，\(f(x, y)\) 在 \(D\) 上是可积的，称这个极限为函数 \(f(x, y)\) 在 \(D\) 上的二重积分，记作：
\[
\begin{array}{l}
\begin{array}{ccc}
\displaystyle \iint_D f(x, y) \, \mathrm{d}A
& \text{or} &
\displaystyle \iint_D f(x, y) \, \mathrm{d}x \, \mathrm{d}y
\end{array}
\\
:= \displaystyle \lim_{||P|| \to 0} \sum_{i=1}^n \sum_{j=1}^m f(\xi_{ij}, \eta_{ij}) \Delta A_{ij} \\
= \displaystyle \lim_{k \to \infty} \sum_{i=1}^k f(\xi_i, \eta_i) \Delta A_i
\end{array}
\]
如果被积分区域 \(D\) 带有弯曲的边界 \(\partial D\)，划分的 小矩形全部位于 \(D\) 内部，而不能覆盖完整的 \(D\)，为了使划分充分地接近 \(D\)，当划分的范数 \(||P|| \to 0\) 时，必须要使得 \(D\) 中不在划分内部的部分的面积趋于零，对于绝大多数的 \(\partial D\)，这是可以做到的，然而在处理分形的边界时，这个问题就会变得复杂。在哪些区域 \(D\) 上能够计算二重积分，这个问题在此处不讨论。
与在一元函数中的积分类似，连续的二元函数在有界闭区域上一定是可积的，这个定理在此处不证明。
本文涉及的所有二重积分都是可积分的。
富比尼定理
定理 若函数 \(f(x, y)\) 在整个矩形区域
\[
D = \{ (x, y) \mid a \leq x \leq b, c \leq y \leq d \}
\]
上连续，则
\[
\iint_D f(x, y) \, \mathrm{d}A = \int_a^b \left( \int_c^d f(x, y) \, \mathrm{d}y \right) \, \mathrm{d}x = \int_c^d \left( \int_a^b f(x, y) \, \mathrm{d}x \right) \, \mathrm{d}y
\]
定理 若函数 \(f(x, y)\) 是区域 \(D\) 上的连续函数：
(1) 若 \(D\) 是由 \(a \leq x \leq b\)，\(g_1(x) \leq y \leq g_2(x)\) 定义的，其中 \(g_1(x)\) 和 \(g_2(x)\) 是 \([a, b]\) 上的连续函数，则
\[
\iint_D f(x, y) \, \mathrm{d}A = \int_a^b \left( \int_{g_1(x)}^{g_2(x)} f(x, y) \, \mathrm{d}y \right) \, \mathrm{d}x
\]
(2) 若 \(D\) 是由 \(h_1(y) \leq x \leq h_2(y)\)，\(c \leq y \leq d\) 定义的，其中 \(h_1(y)\) 和 \(h_2(y)\) 是 \([c, d]\) 上的连续函数，则
\[
\iint_D f(x, y) \, \mathrm{d}A = \int_c^d \left( \int_{h_1(y)}^{h_2(y)} f(x, y) \, \mathrm{d}x \right) \, \mathrm{d}y
\]
这两个定理可以由「物体的体积与计算体积时使用的截面方法无关」直观地理解。其证明在此处不证明。
这两个定理给出将二重积分转化为累次积分的计算方法，对于既不属于 (1) 也不属于 (2) 的区域，可以通过将积分区域划分为若干个满足 (1) 或 (2) 的区域，然后分别计算二重积分，最后求和。使用定义不难证明二重积分对积分区域的有限划分是可加的。
在国内的教材中，属于 (1) 的区域通常被称为 \(x-\) 型区域，属于 (2) 的区域通常被称为 \(y-\) 型区域。
二重积分的性质
基本性质
如果 \(f(x, y)\) 和 \(g(x, y)\) 是连续函数，则：
(1) 线性性之 1 次齐次性，对任意常数 \(k\)：
\[
\iint_D k\cdot f(x, y) \, \mathrm{d}A = k \iint_D f(x, y) \, \mathrm{d}A
\]
(2) 线性性之可加性：
\[
\iint_D \left( f(x, y) \pm g(x, y) \right) \, \mathrm{d}A = \iint_D f(x, y) \, \mathrm{d}A \pm \iint_D g(x, y) \, \mathrm{d}A
\]
(3) 对区间 \(D\) 的可加性，如果 \(D\) 可以分解为两个不相交的区域 \(D_1\) 和 \(D_2\)：
\[
\iint_D f(x, y) \, \mathrm{d}A = \iint_{D_1} f(x, y) \, \mathrm{d}A + \iint_{D_2} f(x, y) \, \mathrm{d}A
\]
(4) 优势积分：如果在区域 \(D\) 上 \(f(x, y) \geq g(x, y)\)，则：
\[
\iint_D f(x, y) \, \mathrm{d}A \geq \iint_D g(x, y) \, \mathrm{d}A
\]
特例：如果在区域 \(D\) 上 \(f(x, y) \geq 0\)，则：
\[
\iint_D f(x, y) \, \mathrm{d}A \geq 0
\]
所有的这些性质都可以通过定义证明。
二重积分的中值定理
定理 如果函数 \(f(x, y)\) 在有界闭区域 \(D\) 上连续，则在区域 \(D\) 上至少存在一点 \((\xi, \eta)\)，使得：
\[
\iint_D f(x, y) \, \mathrm{d}A = f(\xi, \eta) \cdot A(D)
\]
证明. 由于 \(f(x, y)\) 在有界闭区域 \(D\) 上连续，所以在 \(D\) 上一定存在最大值 \(M\) 和最小值 \(m\)，则：
\[
m \cdot A(D) = \iint_D m \, \mathrm{d}A \leq \iint_D f(x, y) \, \mathrm{d}A \leq \iint_D M \, \mathrm{d}A = M \cdot A(D)
\]
因此，\(\displaystyle \frac{1}{A(D)} \iint_D f(x, y) \, \mathrm{d}A\) 是介于 \(m\) 和 \(M\) 之间的一个数。
根据连续函数的介值定理，必然存在 \((\xi, \eta) \in D\)，使得 \(f(\xi, \eta) = \displaystyle \frac{1}{A(D)} \iint_D f(x, y) \, \mathrm{d}A\)。将 \(A(D)\) 乘到等式两边即可得到二重积分的中值定理。\(\blacksquare\)
直角坐标系下二重积分的计算
求积分限的一般过程
求解二重积分 \(\displaystyle \iint_R f(x, y) \, \mathrm{d}A\) 的过程中，首先将积分区域 \(R\) 分解成一个或多个适用富比尼定理的区域（\(x-\) 型区域或 \(y-\) 型区域），然后根据富比尼定理，将二重积分转化为累次积分，最后计算累次积分。应用富比尼定理的过程中，需要注意积分限的确定。
下面给出求解积分 \(\displaystyle \iint_R f(x, y) \, \mathrm{d}A\) 先对 \(y\) 积分后对 \(x\) 积分的一般过程：
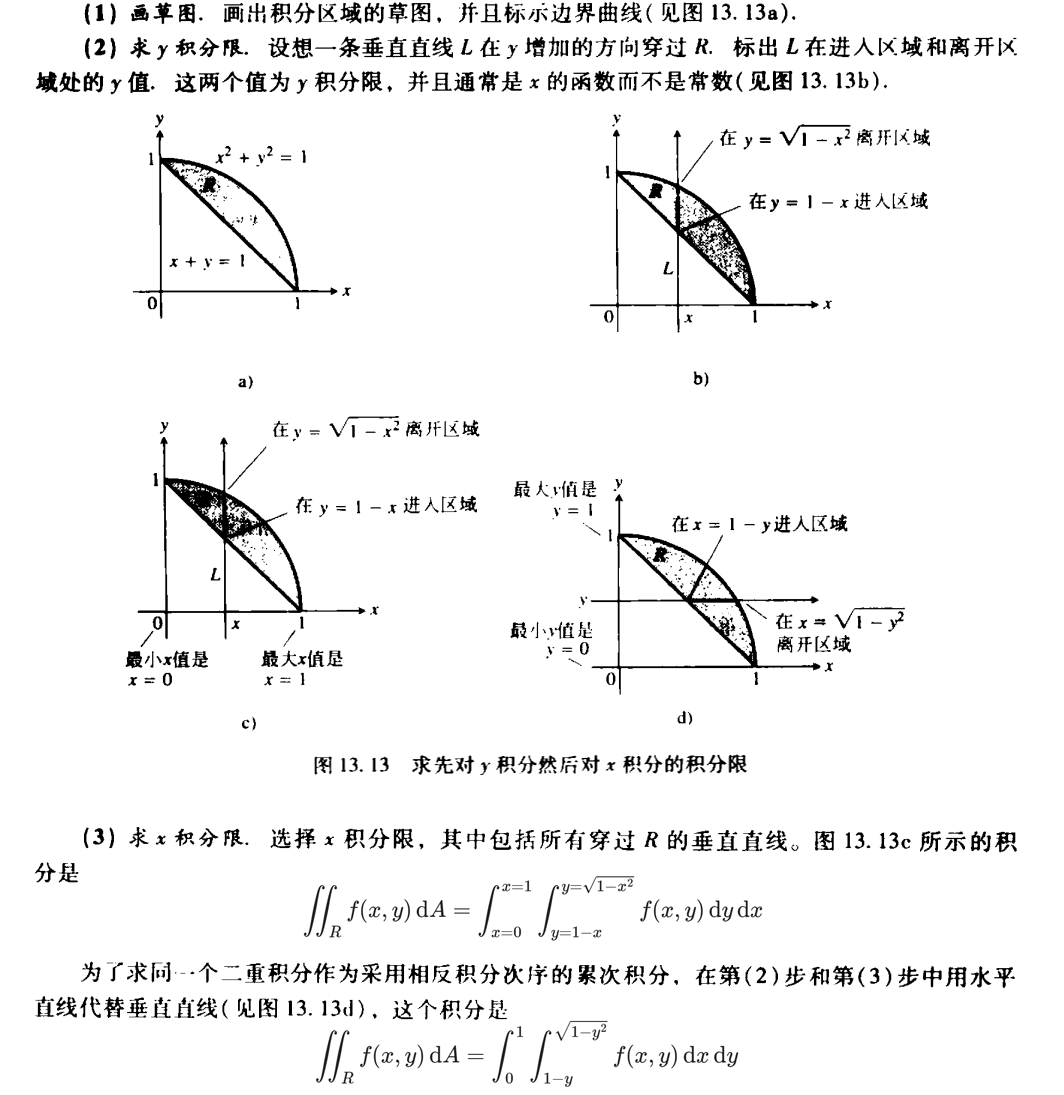
极坐标系下二重积分的计算
使用二重积分的定义在极坐标系下计算二重积分
在直角坐标的情况下，我们有 \(\mathrm{d}A = \mathrm{d}x \, \mathrm{d}y\)，在极坐标系下，我们有 \(\mathrm{d}A = r \, \mathrm{d}r \, \mathrm{d}\theta\)。
使用以原点为圆心的圆弧和以原点为起点的射线构成网格。使用网格中的每一个小矩形（称为极矩形）以与直角坐标系下的小矩形类似的方式覆盖被积分区域 \(D\)，由黎曼和定义二重积分的值：
\[
\iint_D f(x, y) \, \mathrm{d}A = \lim_{k \to \infty} \sum_{i=1}^k f(r_i, \theta_i) \Delta A_i
\]
为了求解这个极限，我们必须用 \(\Delta r_i\) 和 \(\Delta \theta_i\) 来表示 \(\Delta A_i\)，并且极限要求 \(\Delta r_i \to 0\) 和 \(\Delta \theta_i \to 0\)。
如图所示（图中使用 \(\Delta \sigma\) 表示我们所说的 \(\Delta A\)），使用大扇形的面积减去小扇形的面积计算 \(\Delta A_i\)：
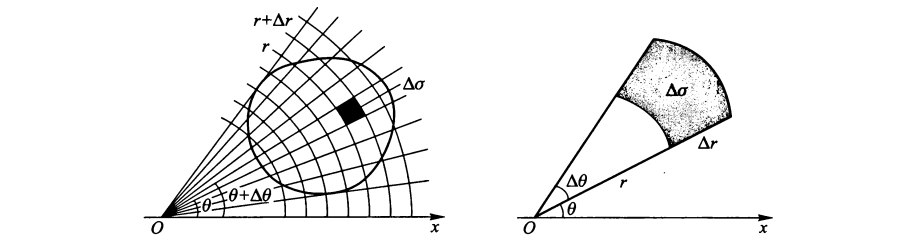
当 \(\Delta r_i \to 0\) 和 \(\Delta \theta_i \to 0\) 时，我们有：
\[
\begin{array}{ll}
\Delta A_i
&= \displaystyle \left( \frac{1}{2} (r_i + \Delta r_i)^2 - \frac{1}{2} r_i^2 \right) \Delta \theta_i \\
&= \displaystyle r_i \Delta r_i \Delta \theta_i + \frac{1}{2}\Delta r_i^2 \Delta \theta_i \\
&= \displaystyle r_i \Delta r_i \Delta \theta_i + o(\Delta r_i \Delta \theta_i)
\end{array}
\]
因此，我们有 \(\mathrm{d}A = r \, \mathrm{d}r \, \mathrm{d}\theta\)。从而，对于极坐标系下的二重积分，我们有：
\[
\iint_D f(x, y) \, \mathrm{d}A = \iint_D f(r \cos \theta, r \sin \theta) \, r \, \mathrm{d}r \, \mathrm{d}\theta
\]
与直角坐标系下的二重积分类似，我们可以使用富比尼定理将极坐标系下的二重积分转化为累次积分：
\[
\iint_D f(x, y) \, \mathrm{d}A = \int_{\theta = \alpha}^{\theta = \beta} \left( \int_{r = g_1(\theta)}^{r = g_2(\theta)} f(r \cos \theta, r \sin \theta) \, r \, \mathrm{d}r \right) \, \mathrm{d}\theta
\]
在极坐标系中求积分限的一般过程
下图给出了在极坐标系中求积分限的一般过程：
也可以先对 \(\theta\) 积分后对 \(r\) 积分，这个时候，应该使用逆时针方向的圆弧（这个圆弧以原点为圆心）穿过积分区域 \(D\) 来求解内层积分的积分限：从 \(\theta = \theta_1(r)\) 到 \(\theta = \theta_2(r)\)。然后求限定 \(D\) 的最小 \(r\) 值和最大 \(r\) 值，从而求解外层积分的积分限。
二重积分的一般换元法
设坐标变换 \(\begin{cases} x = x(u, v) \\ y = y(u, v) \end{cases}\) 将平面区域 \(D\) （以 \((x, y)\) 为坐标）变换为平面区域 \(D'\) （以 \((u, v)\) 为坐标），且满足：
- 变换是一一对应的，即对于 \(D\) 中的每一点 \((x, y)\)，变换后的点 \((u, v)\) 也是唯一的；
- 坐标变换 \(x(u, v)\) 和 \(y(u, v)\) 在 \(D'\) 上有连续的偏导数；
- 变换的雅可比行列式 \(\displaystyle \frac{\partial(x, y)}{\partial (u, v)} = \left| \begin{array}{cc} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{array} \right| \neq 0\)。
则有：
\[
\iint_D f(x, y) \, \mathrm{d}A = \iint_{D'} f(x(u, v), y(u, v)) \left| \frac{\partial(x, y)}{\partial (u, v)} \right| \, \mathrm{d}u \, \mathrm{d}v
\]
此处，\(\displaystyle \left| \frac{\partial(x, y)}{\partial (u, v)} \right|\, \mathrm{d}u \, \mathrm{d}v\) 表示变换后的面积元 \(\mathrm{d}A'\)，而 \(\displaystyle \left| \frac{\partial(x, y)}{\partial (u, v)} \right|\) 表示变换的缩放因子，是雅可比行列式的绝对值。
这个公式在此处不证明。
一些例题
通过交换积分次序简化计算
通过换元法换元至极坐标系下计算
形如 \(f(\sqrt{x^2 + y^2})\)，\(\displaystyle f(\frac{y}{x})\)，\(\displaystyle f(\frac{x}{y})\) 的函数，通过极坐标换元后，可以转化为仅与 \(r\) 有关的函数（第一种情况）和 \(\theta\) 有关的函数（第二、第三种情况），从而简化计算。
与圆有关的积分区域，也可以通过极坐标换元简化计算。
例. 计算 \(\displaystyle \iint_D \sqrt{x^2 + y^2} \, \mathrm{d}A\)，其中区域 \(D\) 为曲线 \(x^2 + y^2 = 2ay\) 围成的区域。
令 \(\begin{cases} x = r \cos \theta \\ y = r \sin \theta \end{cases}\)，则 \(x^2 + y^2 = 2ay\) 变为 \(r = 2a \sin \theta\)。通过画图可以确定，先对 \(r\) 积分再对 \(\theta\) 积分的积分限变为 \(0 \leq r \leq 2a \sin \theta\)，\(0 \leq \theta \leq \pi\)。所以：
\[
\begin{array}{rl}
\displaystyle \iint_D \sqrt{x^2 + y^2} \, \mathrm{d}A
&= \displaystyle \int_0^{\pi} \int_0^{2a \sin \theta} r \, r \, \mathrm{d}r \, \mathrm{d}\theta \\
&= \displaystyle \int_0^{\pi} \left( \int_0^{2a \sin \theta} r^2 \, \mathrm{d}r \right) \, \mathrm{d}\theta \\
&= \displaystyle \int_0^{\pi} \frac{8}{3} a^3 \sin^3 \theta \, \mathrm{d}\theta \\
&= \displaystyle \frac{8}{3} a^3 \int_0^{\pi} \sin^3 \theta \, \mathrm{d}\theta \\
&= \displaystyle \frac{8}{3} \cdot 2 \cdot \int_0^{\textstyle \frac{\pi}{2}} \sin^3 \theta \, \mathrm{d}\theta \\
&= \displaystyle \frac{8}{3} \cdot 2 \cdot \left( \frac{4}{3} \cdot \frac{2}{1} \right) \\
&= \displaystyle \frac{32}{9} a^3
\end{array}
\]
例. 计算 \(\displaystyle \iint_D (x + y) \, \mathrm{d}A\)，其中区域 \(D\) 为曲线 \(x^2 + y^2 = x + y\) 围成的区域。
令 \(\begin{cases} \displaystyle x = \frac{1}{2} + r \cos \theta \\ \displaystyle y = \frac{1}{2} + r \sin \theta \end{cases}\)，则 \(x^2 + y^2 = x + y\) 变为 \(r = 1\)。通过画图可以确定，先对 \(\theta\) 积分再对 \(r\) 积分的积分限变为 \(0 \leq \theta \leq 2\pi\)，\(\displaystyle 0 \leq r \leq \frac{1}{\sqrt{2}}\)。
而由于平移变换不会改变面积元的缩放因子，所以变换的雅可比行列式的绝对值 \(|J| = r\)。所以：
\[
\begin{array}{rl}
\displaystyle \iint_D (x + y) \, \mathrm{d}A
&= \displaystyle \int_0^{2\pi} \int_0^{\frac{1}{\sqrt{2}}} \left( \frac{1}{2} + r \cos \theta + \frac{1}{2} + r \sin \theta \right) r \, \mathrm{d}r \, \mathrm{d}\theta \\
&= \displaystyle \int_0^{2\pi} \int_0^{\frac{1}{\sqrt{2}}} \left[r + (\sin \theta + \cos \theta) r^2\right] \, \mathrm{d}r \, \mathrm{d}\theta \\
&= \displaystyle \int_0^{2\pi} \left[\frac{1}{4} + C(\sin \theta + \cos \theta) \right] \, \mathrm{d}\theta \\
&= \displaystyle \frac{1}{2}\pi + 0 = \frac{1}{2}\pi
\end{array}
\]
通过一般换元法简化计算
需要留意雅可比行列式满足 \(\displaystyle \frac{\partial(x, y)}{\partial (u, v)} \cdot \frac{\partial(u, v)}{\partial (x, y)} = 1\)。有时可以利用这个性质来简化偏导数的计算。
例. 求曲线 \(xy = a^2\)，\(xy = 2a^2\)，\(y = x\)，\(y = 2x\) 围成的区域的面积。
作变换 \(\begin{cases} u = xy \\ \displaystyle v = \frac{y}{x} \end{cases}\)，则有：\(a^2 \leq u \leq 2a^2\)，\(1 \leq v \leq 2\)。计算雅可比行列式：
\[
\frac{\partial(x, y)}{\partial(u, v)}
= \left( \frac{\partial(u, v)}{\partial(x, y)}\right)^{-1}
= \begin{vmatrix}
\displaystyle y &
\displaystyle x \\
\displaystyle -\frac{y}{x^2} &
\displaystyle \frac{1}{x}
\end{vmatrix}^{-1}
= \left( 2\frac{y}{x} \right)^{-1}
= \frac{1}{2v}
\]
设 \(D\) 为原区域，\(D'\) 为变换后的区域，有：
\[
\begin{array}{rl}
\displaystyle \iint_D \, \mathrm{d}A
&= \displaystyle \iint_{D'} \left| \frac{\partial(x, y)}{\partial(u, v)} \right| \, \mathrm{d}u \, \mathrm{d}v \\
&= \displaystyle \int_{a^2}^{2a^2} \int_1^2 \frac{1}{2v} \, \mathrm{d}v \, \mathrm{d}u \\
&=\displaystyle \left( \int_{a^2}^{2a^2}\, \mathrm{d}u \right) \left( \int_1^2 \frac{1}{2v} \, \mathrm{d}v \right) \\
&= \displaystyle \frac{a^2}{2} \ln 2
\end{array}
\]
应用对称性简化计算
函数（与积分区域）的对称性
例. 计算 \(\displaystyle \iint_D x + xyf(x^2 + y^2) \, \mathrm{d}A\)，其中区域 \(D\) 为 \(y = x^3\)，\(y = 1\)，\(x = -1\) 围成的区域。
积分区域如图所示。作辅助线 \(y = -x^3\)，该辅助线将积分区域划分为一个关于 \(x\) 轴对称的区域和一个关于 \(y\) 轴对称的区域。
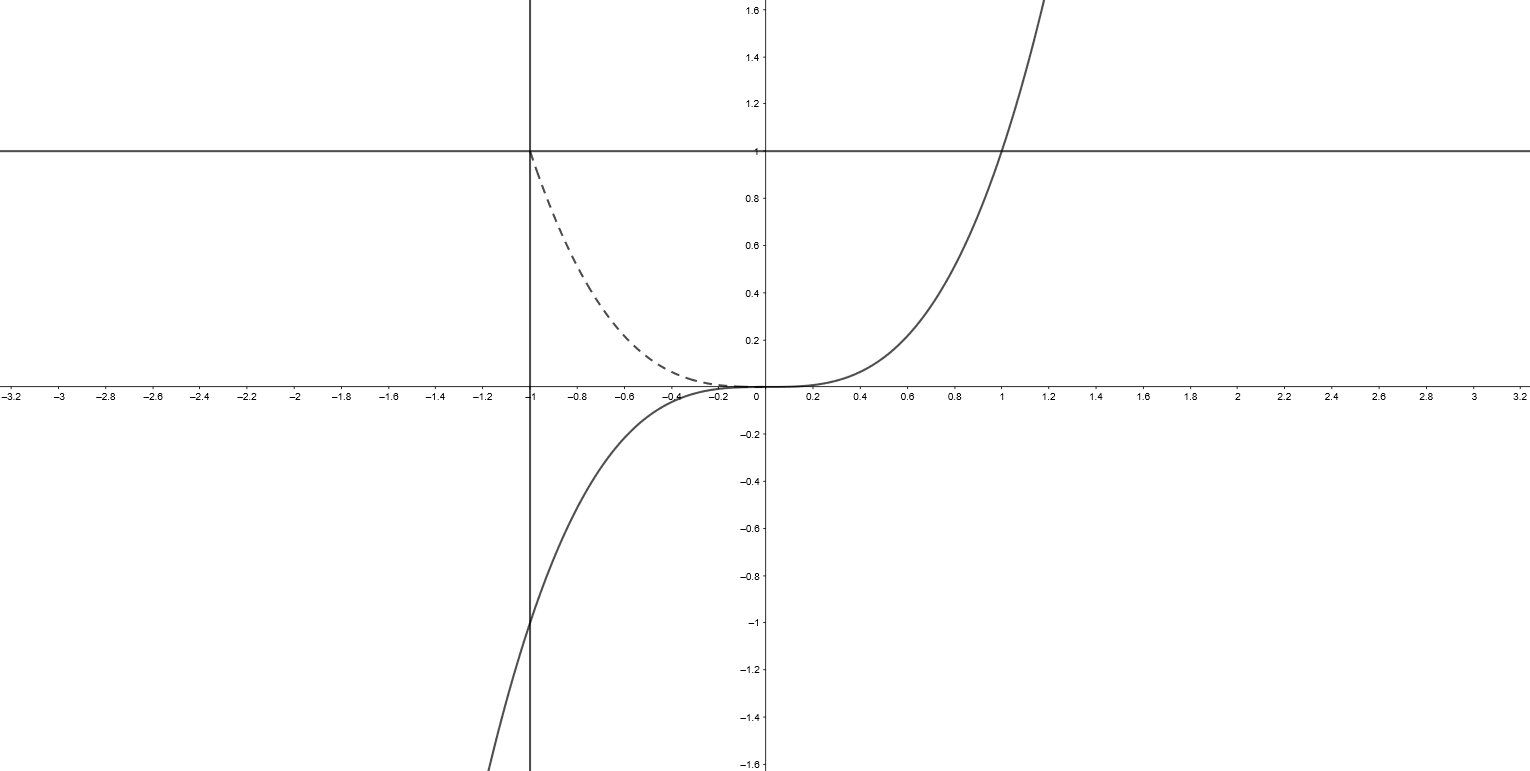
由于函数 \(xyf(x^2 + y^2)\) 对 \(x\) 是奇函数，因此它在关于 \(y\) 轴对称的区域上的二重积分为 \(0\)。由于函数 \(x\) 对 \(y\) 是奇函数，因此它在关于 \(x\) 轴对称的区域上的二重积分为 \(0\)。所以，在整个区域 \(D\) 上：
\[
\iint_D xyf(x^2 + y^2) \, \mathrm{d}A = 0
\]
因此：
\[
\begin{array}{rl}
\displaystyle \iint_D x + xyf(x^2 + y^2) \, \mathrm{d}A
&= \displaystyle \iint_D x \, \mathrm{d}A \\
&= \displaystyle \int_{-1}^1 \int_{x^3}^1 x \, \mathrm{d}y \, \mathrm{d}x \\
&= \displaystyle \int_{-1}^1 x (1 - x^3) \, \mathrm{d}x \\
&= \displaystyle -\frac{2}{5}
\end{array}
\]
例. 计算 \(\displaystyle \iint_D (x + y) \, \mathrm{d}A\)，其中区域 \(D\) 为曲线 \(x^2 + y^2 = x + y\) 围成的区域。
\[
\begin{array}{rl}
\displaystyle \iint_D (x + y) \, \mathrm{d}A
&= \displaystyle \iint_D \left[(x - \frac{1}{2}) + (y - \frac{1}{2}) + 1 \right] \, \mathrm{d}A
\end{array}
\]
由于积分区域关于 \(\displaystyle x = \frac{1}{2}\) 和 \(\displaystyle y = \frac{1}{2}\) 对称，而函数 \(\displaystyle f(x, y) = x - \frac{1}{2}\) 和 \(\displaystyle f(x, y) = y - \frac{1}{2}\) 分别关于 \(\displaystyle x = \frac{1}{2}\) 和 \(\displaystyle y = \frac{1}{2}\) 是奇函数，所以：
\[
\begin{array}{rl}
\displaystyle \iint_D \left[(x - \frac{1}{2}) + (y - \frac{1}{2}) + 1 \right] \, \mathrm{d}A
&= \displaystyle 0 + 0 + \iint_D 1 \, \mathrm{d}A \\
&= \displaystyle \frac{\pi}{2}
\end{array}
\]
变量（与积分区域）的对称性
例. 计算 \(\displaystyle \iint_D \frac{x^2}{a^2} + \frac{y^2}{b^2} \, \mathrm{d}A\)，其中区域 \(D\) 为圆 \(x^2 + y^2 \leq R^2\)。
被积分区域关于直线 \(y = x\) 对称。因此，\(\displaystyle \iint_D f(x, y) \, \mathrm{d}A = \iint_D f(y, x) \, \mathrm{d}A\)。
由变量的对称性，有 \(\displaystyle \iint_D \frac{x^2}{a^2} + \frac{y^2}{b^2} \, \mathrm{d}A = \iint_D \frac{y^2}{a^2} + \frac{x^2}{b^2} \, \mathrm{d}A\)，所以：
\[
\begin{array}{rl}
\displaystyle \iint_D \frac{x^2}{a^2} + \frac{y^2}{b^2} \, \mathrm{d}A
&= \displaystyle \frac{1}{2} \left( \iint_D \frac{x^2}{a^2} + \frac{y^2}{b^2} \, \mathrm{d}A + \iint_D \frac{y^2}{a^2} + \frac{x^2}{b^2} \, \mathrm{d}A \right) \\
&= \displaystyle \frac{1}{2} \left( \frac{1}{a^2} + \frac{1}{b^2} \right) \iint_D (x^2 + y^2) \, \mathrm{d}A \\
&= \displaystyle \frac{1}{2} \left( \frac{1}{a^2} + \frac{1}{b^2} \right) \int_0^{2\pi} \int_0^R r^2 \, r \, \mathrm{d}r \, \mathrm{d}\theta \\
&= \displaystyle \frac{1}{2} \left( \frac{1}{a^2} + \frac{1}{b^2} \right) \int_0^{2\pi} \frac{1}{4} R^4 \, \mathrm{d}\theta \\
&= \displaystyle \frac{1}{2} \left( \frac{1}{a^2} + \frac{1}{b^2} \right) \frac{1}{4} R^4 \cdot 2\pi \\
&= \displaystyle \frac{\pi R^4}{4} \left( \frac{1}{a^2} + \frac{1}{b^2} \right)
\end{array}
\]
使用二重积分计算复杂的一重积分
例. 计算 \(\displaystyle \int_0^{+\infty} e^{-x^2} \, \mathrm{d}x\)。
设 \(\displaystyle I(R) = \int_0^R e^{-x^2} \, \mathrm{d}x\)，则：
\[
\begin{array}{ll}
I^2(R)
&= \displaystyle \left( \int_0^R e^{-x^2} \, \mathrm{d}x \right) \left( \int_0^R e^{-y^2} \, \mathrm{d}y \right) \\
&= \displaystyle \int_0^R \left( \int_0^R e^{-x^2} e^{-y^2} \, \mathrm{d}y \right) \, \mathrm{d}x \\
&= \displaystyle \iint_{[0, R] \times [0, R]} e^{-(x^2+y^2)} \, \mathrm{d}x \, \mathrm{d}y \\
&= \displaystyle \iint_D e^{-r^2} \, r \, \mathrm{d}r \, \mathrm{d}\theta \\
\end{array}
\]
被积分区域 \(D = [0, R] \times [0, R]\)（直角坐标）介于以原点为圆心，以 \(R\) 和 \(\sqrt{2}R\) 为半径的两个四分之一圆之间，而被积函数 \(e^{-(x^2+y^2)}\) 恒正，所以：
\[
\int_0^{\textstyle \frac{\pi}{2}} \left( \int_0^R e^{-r^2} \, r \, \mathrm{d}r \right) \, \mathrm{d}\theta
< \iint_D e^{-r^2} \, r \, \mathrm{d}r \, \mathrm{d}\theta
< \int_0^{\textstyle \frac{\pi}{2}} \left( \int_0^{\sqrt{2}R} e^{-r^2} \, r \, \mathrm{d}r \right) \, \mathrm{d}\theta
\]
又因为
\[
\begin{array}{rl}
\displaystyle \int_0^{\textstyle \frac{\pi}{2}} \left( \int_0^R e^{-r^2} \, r \, \mathrm{d}r \right) \, \mathrm{d}\theta
&= \displaystyle \left( -\frac{1}{2}\int_0^R e^{-r^2} \, \mathrm{d}(-r^2) \right) \left( \int_0^{\textstyle \frac{\pi}{2}} \, \mathrm{d}\theta \right)\\
&= \displaystyle \frac{\pi}{4} \left( 1 - e^{-R^2} \right)
\end{array}
\]
当 \(R \to +\infty\) 时，使用夹逼定理，有 \(\displaystyle I^2(R) \to \frac{\pi}{4}\)，所以：
\[
\int_0^{+\infty} e^{-x^2} \, \mathrm{d}x = \frac{\sqrt{\pi}}{2}
\]
Note
上式中的第二个等号是因为：
\[
\begin{array}{ll}
\displaystyle \int_0^R \left( \int_0^R e^{-x^2} e^{-y^2} \, \mathrm{d}y \right) \, \mathrm{d}x
&= \displaystyle \int_0^R e^{-x^2} \left( \int_0^Re^{-y^2} \, \mathrm{d}y \right) \, \mathrm{d}x \\
&= \displaystyle \left( \int_0^R e^{-y^2} \, \mathrm{d}y \right) \left(\int_0^R e^{-x^2} \, \mathrm{d}x\right)
\end{array}
\]
在对 \(x\) 的积分中，所有与 \(y\) 有关的项都被看作常数，所以可以提出来。这在某些条件下能够将累次积分转为两个一重积分的乘积。
例. 计算 \(\displaystyle \int_0^1 \frac{x^p - x^q}{\ln x} \, \mathrm{d}x\)。
\[
\begin{array}{rl}
\displaystyle \int_0^1 \frac{x^p - x^q}{\ln x} \, \mathrm{d}x
&= \displaystyle \int_0^1 \left( \int_q^p x^y \, \mathrm{d}y\right) \, \mathrm{d}x \\
&= \displaystyle \int_q^p \left( \int_0^1 x^y \, \mathrm{d}x \right) \, \mathrm{d}y \\
&= \displaystyle \int_q^p \frac{1}{y+1} \, \mathrm{d}y \\
&= \displaystyle \ln \frac{p+1}{q+1}
\end{array}
\]