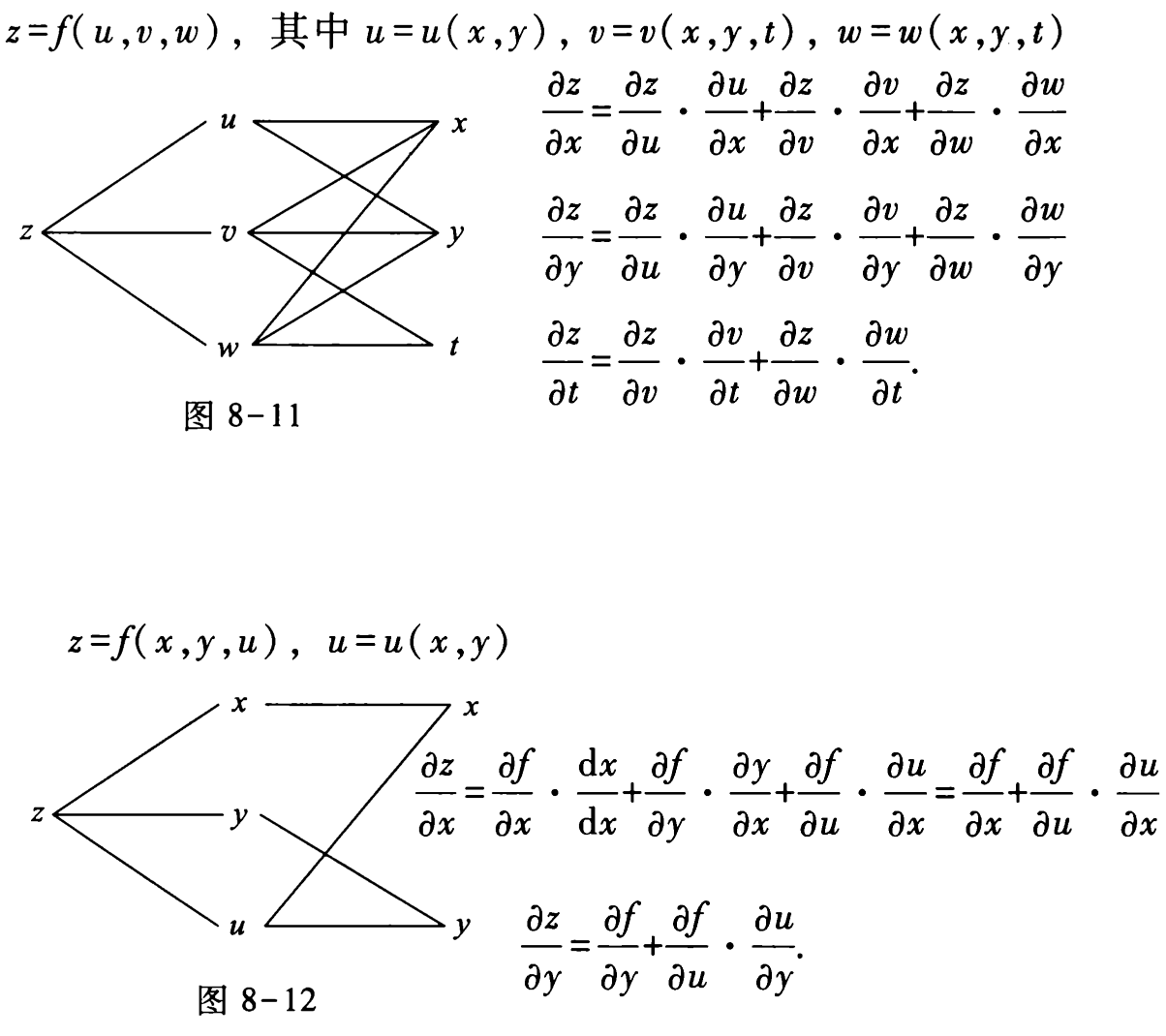多元函数的导数与微分

本文详细介绍了多元函数的导数与微分的基本概念和计算方法。首先定义了多元函数的偏导数，解释了全增量和偏增量的概念，并给出了偏导数的定义和计算方法。接着，讨论了高阶偏导数与混合偏导数，介绍了它们的定义和计算技巧，并证明了混合偏导数在一定条件下可以交换次序。随后，文章探讨了多元函数的全微分，定义了全微分的概念，并讨论了可微性与连续性、可微性与可导性的关系。文章还介绍了复合函数的求导法（链式法则），并通过实例说明了其应用。最后，讨论了隐函数求导法则、场的方向导数与梯度、多元函数的泰勒公式以及多元函数的极值与最值的求法，包括无条件极值和条件最值（拉格朗日乘数法）。通过本文的学习，读者可以全面掌握多元函数导数与微分的基本理论和计算技巧，为进一步研究和应用奠定坚实的基础。

（摘要由 OpenAI GPT 4o 生成）

多元函数的偏导数

偏导数的定义

全增量 $\Delta z = f(x, y) - f(x_0, y_0)$。

偏增量 $\Delta_x z = f(x, y) - f(x_0, y)$；$\Delta_y z = f(x, y) - f(x, y_0)$。

定义 设二元函数 $z = f(x, y)$ 在点 $(x_0, y_0)$ 的某个邻域内有定义，若极限

$$\lim_{\Delta x \rightarrow 0} \frac{\Delta z}{\Delta x} = \lim_{\Delta x \rightarrow 0} \frac{f(x_0 + \Delta x, y_0) - f(x_0, y_0)}{\Delta x} = \lim_{x \rightarrow x_0} \frac{f(x, y_0) - f(x_0, y_0)}{x - x_0}$$

存在，则称此极限为函数 $z = f(x, y)$ 在点 $(x_0, y_0)$ 处对 $x$ 的偏导数，记作 $\displaystyle f'_x(x_0, y_0)$ 或 $\displaystyle \frac{\partial}{\partial x} f \bigg|_{(x_0, y_0)}$ 或 $\displaystyle z'_x(x_0, y_0)$ 或 $\displaystyle \frac{\partial z}{\partial x} \bigg|_{(x_0, y_0)}$。

否则称函数 $z = f(x, y)$ 在点 $(x_0, y_0)$ 处对 $x$ 的偏导数不存在。

对 $y$ 的偏导数定义类似。

如果二元函数 $z = f(x, y)$ 在区域 $G$ 上的每一点 $(x, y)$ 极限 $\displaystyle \lim_{\Delta x \rightarrow 0} \frac{\Delta z}{\Delta x}$ 都存在，则称 $f(x, y)$ 在 $G$ 上对 $x$ 可导，称通过此极限得到的关于 $x, y$ 的函数为函数 $z = f(x, y)$ 对 $x$ 的偏导函数，记作 $\displaystyle f'_z(x, y)$ 或 $\displaystyle \frac{\partial}{\partial x} f(x, y)$。

计算对 $x$ 的偏导函数时，根据偏导数的定义，这等价于：将 $y$ 视为常数，在得到的关于 $x$ 的一元函数中对 $x$ 求导。

因此，一元函数的求导法则可以直接应用于多元函数的偏导数的计算。

计算二元函数 $z = f(x, y)$ 在点 $(x_0, y_0)$ 处对 $x$ 的偏导数时，可以先代入 $y = y_0$，得到一元函数 $z = f(x, y_0)$，再对 $x$ 求导，从而简化计算。

高阶偏导数与混合偏导数

二元函数的偏导数仍然是二元函数，因此可以继续对其求偏导数。假设二元函数 $z = f(x, y)$ 的一阶偏导函数 $\displaystyle \frac{\partial z}{\partial x}$ 、$\displaystyle \frac{\partial z}{\partial y}$ 都存在，则可以继续对其求偏导数，得到二阶偏导数：

$$\begin{array}{c} \displaystyle \frac{\partial}{\partial x}\frac{\partial z}{\partial x} & \displaystyle \frac{\partial}{\partial y}\frac{\partial z}{\partial x} && \displaystyle \frac{\partial}{\partial x}\frac{\partial z}{\partial y} & \displaystyle \frac{\partial}{\partial y}\frac{\partial z}{\partial y} \end{array}$$

依次记作：

$$\begin{array}{c} \displaystyle \frac{\partial^2 z}{\partial x^2} & \displaystyle \frac{\partial^2 z}{\partial x \partial y} && \displaystyle \frac{\partial^2 z}{\partial y \partial x} & \displaystyle \frac{\partial^2 z}{\partial y^2} \end{array}$$

或者

$$\begin{array}{c} \displaystyle f''_{xx}(x, y) & \displaystyle f''_{xy}(x, y) && \displaystyle f''_{yx}(x, y) & \displaystyle f''_{yy}(x, y) \end{array}$$

定理 若二元函数 $z = f(x, y)$ 的二阶偏导数 $f''_{xy}(x, y)$ 和 $f''_{yx}(x, y)$ 都在 $(x_0, y_0)$ 处连续，则有 $f''_{xy}(x_0, y_0) = f''_{yx}(x_0, y_0)$。

证明.

由于 $f''_{xy}(x, y)$、$f''_{yx}(x, y)$ 在 $(x_0, y_0)$ 处连续，因此这两个函数在 $(x_0, y_0)$ 的邻域内有定义，取充分小的 $\Delta x$，$\Delta y$（$\Delta x$，$\Delta y$ 均不为 $0$），可以使得 $(x_0 + \Delta x, y_0)$、$(x_0, y_0 + \Delta y)$、$(x_0 + \Delta x, y_0 + \Delta y)$ 三点均在 $(x_0, y_0)$ 的邻域内。

令 $\varphi(x) = f(x, y_0 + \Delta y) - f(x, y_0)$，$\psi(y) = f(x_0 + \Delta x, y) - f(x_0, y)$。

对 $\varphi(x)$ 使用拉格朗日中值定理，有 $\varphi(x) = f'_y(x, y_0 + \theta_1 \Delta y) \Delta y$，其中 $\theta _1 \in (0, 1)$。

Note

此处拉格朗日中值定理适用的原因是：对于每一个固定的 $x$，关于 $y$ 的一元函数 $f(x, y)$ 在闭区间 $y \in [y_0, y_0 + \Delta y]$ 上连续且在开区间 $y \in (y_0, y_0 + \Delta y)$ 可导。

由于 $f(x, y)$ 在点 $(x_0, y_0)$ 处二阶可导，必然存在一个邻域，使得 $f(x, y)$ 在该邻域内一阶可导。

同理，对 $\psi(y)$ 使用拉格朗日中值定理，有 $\psi(y) = f'_x(x_0 + \theta_2 \Delta x, y) \Delta x$，其中 $\theta _2 \in (0, 1)$。

考虑

$$W = f(x_0 + \Delta x, y_0 + \Delta y) - f(x_0 + \Delta x, y_0) - f(x_0, y_0 + \Delta y) + f(x_0, y_0)$$

有 $W = \varphi(x_0 + \Delta x) - \varphi(x_0) = \psi(y_0 + \Delta y) - \psi(y_0)$。

对 $\varphi(x_0 + \Delta x) - \varphi(x_0)$ 使用一元函数的拉格朗日中值定理，得到 $\varphi(x_0 + \Delta x) - \varphi(x_0) = \varphi'_x(x_0 + \theta _3 \Delta x) \Delta x$，其中 $\theta _3 \in (0, 1)$。

Note

此处拉格朗日中值定理适用的原因是：$\varphi(x) = f'_y(x, y_0 + \theta_1 \Delta y) \Delta y$

由于 $f(x, y)$ 在点 $(x_0, y_0)$ 处二阶可导，必然存在一个邻域，使得 $f(x, y)$ 在该邻域内一阶偏导数连续可导。

整理可得：$W = f''_{yx}(x_0 + \theta _3\Delta x, y_0 + \theta_1 \Delta y) \Delta y \Delta x$。

同理，对 $\psi(y_0 + \Delta y) - \psi(y_0)$ 使用一元函数的拉格朗日中值定理，得到 $\psi(y_0 + \Delta y) - \psi(y_0) = \psi'_y(y_0 + \theta _4 \Delta y) \Delta y$，其中 $\theta _4 \in (0, 1)$。

整理可得：$W = f''_{xy}(x_0 + \theta _2\Delta x, y_0 + \theta_4 \Delta y) \Delta y \Delta x$。

因此，有 $f''_{xy}(x_0 + \theta _2\Delta x, y_0 + \theta_4 \Delta y) = f''_{yx}(x_0 + \theta _3\Delta x, y_0 + \theta_1 \Delta y) = A$。

当 $\Delta x \rightarrow 0$，$\Delta y \rightarrow 0$ 时，有 $A = f''_{xy}(x_0 + \theta _2\Delta x, y_0 + \theta_4 \Delta y) \rightarrow f''_{xy}(x_0, y_0)$。因为 $f''_{xy}(x, y)$ 在 $(x_0, y_0)$ 处连续，所以 $A = f''_{xy}(x_0, y_0)$。

同理，$A = f''_{yx}(x_0, y_0)$。

因此，$f''_{xy}(x_0, y_0) = f''_{yx}(x_0, y_0)$。$\blacksquare$

同理可证，对于更高维度的多元函数和更高的求导阶数，只要偏导函数在 $(x_0, y_0, \dots)$ 处连续，那么混合偏导的值与求导的顺序无关。

多元函数的全微分

一元函数的微分

若 $\Delta y = f(x_0 + \Delta x) - f(x_0) = A \cdot \Delta x + \omicron(\Delta x)$，称函数 $f(x)$ 在 $x_0$ 可微，$A \cdot \Delta x$ 为该点的微分，用记号 $dy$ 表示。

我们探究一元函数中可微和可导的关系：

若函数 $y = f(x)$ 在 $x_0$ 处可微，则在 $x_0$ 处，有 $\Delta y - A \cdot \Delta x = \omicron(\Delta x)$，即 $\displaystyle \lim_{\Delta x \rightarrow 0} \frac{\Delta y - A \cdot \Delta x}{\Delta x} = 0$，也即 $\displaystyle \lim_{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x} = A$。这恰好是函数 $y = f(x)$ 在 $x_0$ 处导数值的定义。

因此，一元函数在某点可微和在该点可导是等价的。

多元函数的全微分

定义 若二元函数 $z = f(x, y)$ 在点 $(x_0, y_0)$ 处的全增量 $\Delta z = f(x_0 + \Delta x, y_0 + \Delta y) - f(x_0, y_0)$ 可表示为

$$\Delta z = A \Delta x + B \Delta y + \omicron(\rho)\quad (\rho := \sqrt{(\Delta x)^2 + (\Delta y)^2},\ \Delta x,\ \Delta y \rightarrow 0)$$

并且 $A$、$B$ 与 $\Delta x$、$\Delta y$ 无关，称函数 $z = f(x, y)$ 在点 $(x_0, y_0)$ 处可微，$A \Delta x + B \Delta y$ 为该点的全微分，用记号 $\mathrm{d}z$ 表示。

Note

上式 $\Delta z = A \Delta x + B \Delta y + \omicron(\rho)$ 存在若干种等价形式，包括不涉及 $\Delta x$、$\Delta y$ 的形式，此处不一一列举。

定理 若二元函数 $z = f(x, y)$ 在点 $(x_0, y_0)$ 处可微，则有二元函数 $z = f(x, y)$ 在点 $(x_0, y_0)$ 处连续。（可微一定连续）

证明.

$$\begin{array}{rl} \displaystyle \lim_{\substack{x \rightarrow x_0 \\ y \rightarrow y_0}} f(x, y) &= \displaystyle \lim_{\substack{\Delta x \rightarrow 0 \\ \Delta y \rightarrow 0}} f(x_0 + \Delta x, y_0 + \Delta y) \\ &= \displaystyle \lim_{\substack{\Delta x \rightarrow 0 \\ \Delta y \rightarrow 0}} \left( \Delta z + f(x_0, y_0) \right) \\ &= \displaystyle \lim_{\substack{\Delta x \rightarrow 0 \\ \Delta y \rightarrow 0}} \left( A \Delta x + B \Delta y + \omicron(\rho)\right)+ f(x_0, y_0) \\ &= f(x_0, y_0) \quad \blacksquare \end{array}$$

定理 若二元函数 $z = f(x, y)$ 在点 $(x_0, y_0)$ 处可微，则 $z = f(x, y)$ 在点 $(x_0, y_0)$ 处的两个偏导数 $f'_x(x_0, y_0)$，$f'_y(x_0, y_0)$ 均存在，且有 $f'_x(x_0, y_0) = A$，$f'_y(x_0, y_0) = B$。（可微一定可导）

证明.

由于 $z = f(x, y)$ 在点 $(x_0, y_0)$ 处可微，因此有 $\Delta z = A \Delta x + B \Delta y + \omicron(\rho)$。令 $\Delta y = 0$，则有 $\Delta z = A \Delta x + \omicron(|\Delta x|)$，以及 $\Delta z = f(x_0 + \Delta x, y_0) - f(x_0, y_0) = \Delta_x z$。

因此：

$$f'_x(x_0, y_0) = \lim_{\Delta x \rightarrow 0} \frac{\Delta_x z}{\Delta x} = \lim_{\Delta x \rightarrow 0} \frac{A \Delta x + \omicron(|\Delta x|)}{\Delta x} = A$$

同理，令 $\Delta x = 0$，有 $f'_y(x_0, y_0) = B$。$\blacksquare$

然而，可导不一定可微。例如，函数 $f(x, y) = |x| + |y|$ 在点 $(0, 0)$ 处可导，但不可微。

例如函数 $f(x, y) = \begin{cases}\displaystyle \frac{xy}{x^2 + y^2}, & (x, y) \neq (0, 0) \\0, & (x, y) = (0, 0)\end{cases}$，在点 $(0, 0)$ 处的偏导数：

$$\begin{array}{ll} \displaystyle f'_x(0, 0) &= \displaystyle \lim_{h \to 0} \frac{f(h, 0) - f(0, 0)}{h} \\ &= \displaystyle \lim_{h \to 0} \frac{\frac{0}{h^2} - 0}{h} = 0 \\ \displaystyle f'_y(0, 0) &= \displaystyle \lim_{h \to 0} \frac{f(0, h) - f(0, 0)}{h} \\ &= \displaystyle \lim_{h \to 0} \frac{\frac{0}{h^2} - 0}{h} = 0 \end{array}$$

而在点 $(0, 0)$ 处，极限

$$\begin{array}{ll} \displaystyle \lim_{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{[f(x, y) - 0] - [f'_x(0, 0) \cdot (x - 0) + f'_y(0, 0) \cdot (y - 0)]}{\sqrt{(x - 0)^2 + (y - 0)^2}} &= \displaystyle \lim_{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{\frac{xy}{x^2 + y^2} - 0}{\sqrt{x^2 + y^2}} \\ &= \displaystyle \lim_{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{xy}{(x^2 + y^2)^{3/2}} \end{array}$$

选取路径 $y = x$，有 $\displaystyle \lim_{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{xy}{(x^2 + y^2)^{3/2}} = \lim_{x \rightarrow 0} \frac{x^2}{(2x^2)^{3/2}} = \frac{1}{2^{3/2}x} \rightarrow \infty$；

选取路径 $y = x^2$，有 $\displaystyle \lim_{\substack{x \rightarrow 0 \\ y \rightarrow 0}} \frac{xy}{(x^2 + y^2)^{3/2}} = \lim_{x \rightarrow 0} \frac{1}{(1 + x^2)^{3/2}} = 1$。

从而上述二重极限不存在，因此函数 $f(x, y)$ 在点 $(0, 0)$ 处不可微。

判断二元函数在某点是否可微的一般方法

根据微分的定义：

1. 计算偏导数 $f'_x(x_0, y_0)$，$f'_y(x_0, y_0)$ 是否存在（先排除简单的微分不存在的情况，同理可以通过判断连续性排除一些情况）；
2. 如果偏导数存在，计算极限 $\displaystyle \lim_{\substack{\Delta x \rightarrow 0 \\ \Delta y \rightarrow 0}} \frac{\Delta z - f'_x(x_0, y_0) \Delta x - f'_y(x_0, y_0) \Delta y}{\sqrt{(\Delta x)^2 + (\Delta y)^2}}$ 是否为 $0$。

定理 如果二元函数 $z = f(x, y)$ 的偏导数 $f'_x(x, y)$，$f'_y(x, y)$ 在点 $(x_0, y_0)$ 处连续，则 $z = f(x, y)$ 在点 $(x_0, y_0)$ 处可微。（可微的充分条件）

证明.

$$\begin{array}{ll} \displaystyle \Delta z \displaystyle &= f(x_0 + \Delta x, y_0 + \Delta y) - f(x_0, y_0) \\ &= \displaystyle f(x_0 + \Delta x, y_0 + \Delta y) - f(x_0 + \Delta x, y_0) + f(x_0 + \Delta x, y_0) - f(x_0, y_0) \\ &= \displaystyle f'_y(x_0 + \Delta x, y_0 + \theta_1 \Delta y) \Delta y + f'_x(x_0 + \theta_2 \Delta x, y_0) \Delta x \quad (\theta_1, \theta_2 \in (0, 1)) \end{array}$$

由于 $f'_x(x, y)$，$f'_y(x, y)$ 在点 $(x_0, y_0)$ 处连续，因此有 $\displaystyle \lim_{\substack{\Delta x \rightarrow 0 \\ \Delta y \rightarrow 0}} f'_y(x_0 + \Delta x, y_0 + \theta_1 \Delta y) = f'_y(x_0, y_0)$，$\displaystyle \lim_{\substack{\Delta x \rightarrow 0 \\ \Delta y \rightarrow 0}} f'_x(x_0 + \theta_2 \Delta x, y_0) = f'_x(x_0, y_0)$。

有 $\displaystyle f'_y(x_0 + \Delta x, y_0 + \theta_1 \Delta y) = f'_y(x_0, y_0) + \omicron(\Delta x, \Delta y)$，$\displaystyle f'_x(x_0 + \theta_2 \Delta x, y_0) = f'_x(x_0, y_0) + \omicron(\Delta x, \Delta y)$。

因此 $\Delta z = f'_y(x_0, y_0) \Delta y + f'_x(x_0, y_0) \Delta x + \omicron(\Delta x, \Delta y) \Delta x + \omicron(\Delta x, \Delta y) \Delta y$。

而

$$\lim_{\substack{\Delta x \rightarrow 0 \\ \Delta y \rightarrow 0}} \frac{\omicron(\Delta x, \Delta y) \Delta x + \omicron(\Delta x, \Delta y) \Delta y}{\sqrt{(\Delta x)^2 + (\Delta y)^2}} = 0 + 0 = 0$$

因此 $\Delta z = f'_y(x_0, y_0) \Delta y + f'_x(x_0, y_0) \Delta x + \omicron(\rho)$，即 $z = f(x, y)$ 在点 $(x_0, y_0)$ 处可微。$\blacksquare$

在上面的式子中，由全微分的定义 $\mathrm{d}z := A \Delta x + B \Delta y$，有

$$\mathrm{d}z = \frac{\partial z}{\partial x} \mathrm{d}x + \frac{\partial z}{\partial y} \mathrm{d}y$$

定理 若 $P(x, y)$ 和 $Q(x, y)$ 的偏导数存在且连续，则微分式 $\mathrm{d}z = P(x, y) \mathrm{d}x + Q(x, y) \mathrm{d}y$ 是某个函数的全微分的充要条件是 $\displaystyle \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}$。

证明.

充分性（$\Rightarrow$）：设 $\mathrm{d}z = P(x, y) \mathrm{d}x + Q(x, y) \mathrm{d}y$ 是函数 $f(x, y)$ 的全微分，那么

$$\begin{array}{c} \displaystyle \frac{\partial P}{\partial y} = \frac{\partial}{\partial y} \frac{\partial f}{\partial x} = \frac{\partial^2 f}{\partial x \partial y} \\ \displaystyle \frac{\partial Q}{\partial x} = \frac{\partial}{\partial x} \frac{\partial f}{\partial y} = \frac{\partial^2 f}{\partial y \partial x} \end{array}$$

由 $P(x, y)$ 和 $Q(x, y)$ 的偏导数连续，从而 $\displaystyle \frac{\partial^2 f}{\partial x \partial y}$ 和 $\displaystyle \frac{\partial^2 f}{\partial y \partial x}$ 也是连续函数，连续的混合偏导数可以交换次序，因此 $\displaystyle \frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x}$，从而 $\displaystyle \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x}$。

必要性（$\Leftarrow$）：设 $\displaystyle \frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x} = g(x, y)$，只需要证明对 $g(x, y)$ 的二重积分 $\displaystyle \int \int g(x, y) \mathrm{d}x \mathrm{d}y$ 和 $\displaystyle \int \int g(x, y) \mathrm{d}y \mathrm{d}x$ 的结果相同，这样就能够找到全微分恰为 $\mathrm{d}z = P(x, y) \mathrm{d}x + Q(x, y) \mathrm{d}y$ 的函数 $f(x, y)$。

TODO

证明细节

由充分性和必要性，得证。$\blacksquare$

复合函数求导法（链式法则）

定理 若二元函数 $z = f(u, v) = f(\varphi(x, y), \psi(x, y))$ 在点 $(u, v) = (\varphi(x, y), \psi(x, y))$ 处可微，并且函数 $u = \varphi(x, y)$ 和 $v = \psi(x, y)$ 在点 $(x, y)$ 的偏导数都存在，则复合函数 $z = f(\varphi(x, y), \psi(x, y))$ 在点 $(x, y)$ 处的偏导数都存在，并且有：（链式法则）

$$\begin{array}{ll} \displaystyle \frac{\partial z}{\partial x} &= \displaystyle \frac{\partial z}{\partial u} \frac{\partial u}{\partial x} + \frac{\partial z}{\partial v} \frac{\partial v}{\partial x} \\ \displaystyle \frac{\partial z}{\partial y} &= \displaystyle \frac{\partial z}{\partial u} \frac{\partial u}{\partial y} + \frac{\partial z}{\partial v} \frac{\partial v}{\partial y} \end{array}$$

证明. 由于 $z = f(u, v)$ 在点 $(u, v) = (\varphi(x, y), \psi(x, y))$ 处可微，因此 $z$ 在点 $(u, v)$ 处的全增量

$$\Delta z = \frac{\partial z}{\partial u} \Delta u + \frac{\partial z}{\partial u} \Delta v + \varepsilon_1 \Delta u + \varepsilon_2 \Delta v$$

其中 $\displaystyle \lim_{\substack{\Delta u \rightarrow 0 \\ \Delta v \rightarrow 0}} \varepsilon_1 = 0$，$\displaystyle \lim_{\substack{\Delta u \rightarrow 0 \\ \Delta v \rightarrow 0}} \varepsilon_2 = 0$。

展开有

$$f(\varphi(x', y'), \psi(x', y')) - f(\varphi(x, y), \psi(x ,y)) = \frac{\partial z}{\partial u} (\varphi(x', y') - \varphi(x, y)) + \frac{\partial z}{\partial v} (\psi(x', y') - \psi(x, y)) + \varepsilon_1 \Delta u + \varepsilon_2 \Delta v$$

作换元 $\begin{cases}\varphi(x', y') - \varphi(x, y) = \varphi(x + \Delta x, y) - \varphi(x, y) \\ \psi(x', y') - \psi(x, y) = \psi(x, y + \Delta y) - \psi(x, y)\end{cases}$，有

$$\begin{array}{rl} \displaystyle f(\varphi(x + \Delta x, y), \psi(x + \Delta x, y)) - f(\varphi(x, y), \psi(x ,y)) &= \displaystyle \frac{\partial z}{\partial u} \varphi(x + \Delta x, y) - \varphi(x, y) + \frac{\partial z}{\partial v} \psi(x, y + \Delta y) - \psi(x, y) + \varepsilon_1 \Delta u + \varepsilon_2 \Delta v \\ \displaystyle \Delta_x z &= \displaystyle \frac{\partial z}{\partial u} \Delta_x u + \frac{\partial z}{\partial v} \Delta_x v + \varepsilon_1 \Delta u + \varepsilon_2 \Delta v \end{array}$$

当 $\Delta x \rightarrow 0$ 时，有 $\Delta u \rightarrow 0$，$\Delta v \rightarrow 0$，因此 $\displaystyle \lim_{\Delta x \rightarrow 0} \varepsilon_1 = 0$，$\displaystyle \lim_{\Delta x \rightarrow 0} \varepsilon_2 = 0$。

因此：

$$\begin{array}{rl} \displaystyle \frac{\partial z}{\partial x} &= \displaystyle \lim_{\Delta x \rightarrow 0} \frac{\Delta_x z}{\Delta x} \\ &= \displaystyle \lim_{\Delta x \rightarrow 0} \frac{\frac{\partial z}{\partial u} \Delta_x u + \frac{\partial z}{\partial v} \Delta_x v + \varepsilon_1 \Delta u + \varepsilon_2 \Delta v}{\Delta x} \\ &= \displaystyle \frac{\partial z}{\partial u} \lim_{\Delta x \rightarrow 0} \frac{\Delta_x u}{\Delta x} + \frac{\partial z}{\partial v} \lim_{\Delta x \rightarrow 0} \frac{\Delta_x v}{\Delta x} + 0 + 0 \end{array}$$

又因为函数 $u = \varphi(x, y)$ 和 $v = \psi(x, y)$ 在点 $(x, y)$ 的偏导数都存在，因此有 $\displaystyle \lim_{\Delta x \rightarrow 0} \frac{\Delta_x u}{\Delta x} = \frac{\partial u}{\partial x}$，$\displaystyle \lim_{\Delta x \rightarrow 0} \frac{\Delta_x v}{\Delta x} = \frac{\partial v}{\partial x}$。

从而 $\displaystyle \frac{\partial z}{\partial x} = \frac{\partial z}{\partial u} \frac{\partial u}{\partial x} + \frac{\partial z}{\partial v} \frac{\partial v}{\partial x}$。对 $\displaystyle \frac{\partial z}{\partial y}$ 同理。$\blacksquare$

链式法则的图示法

链式法则可以用下图表示¹：

Note

复合函数的偏导，需要区分先代入后求导，或是先求导后代入。采用某些表达时，可能会造成歧义。

例如，表达式 $f'_x(x, 2x)$ ，如果未加以说明，难以区分是下面两种情况的哪一种：

1. 先在 $f(x, y)$ 中代入 $(x, 2x)$，然后对 $x$ 求导，即 $\displaystyle \frac{d}{dx}[f(x, 2x)]$；
2. 先对 $f(x, y)$ 求 $x$ 的偏导，然后再偏导函数 $f'_x(x, y)$ 中代入 $(x, 2x)$，即 $f_1'(x, 2x)$。

为了消歧义：

对 (1) 使用重命名，令 $z = f(x, 2x)$，然后使用 $\displaystyle \frac{dz}{dx}$ ；

对 (2) 使用下标 $\_ i$ 来表示对多元函数的第 $i$ 个变量求导。

同样地，对复合函数 $u = F(x + y, x y)$ ，符号 $\displaystyle \frac{\partial F}{\partial x}$ 可能会产生歧义：是 (1) 代入 $(x + y, xy)$ 之后，$F$ 对 $x$ 的偏导数 或是 (2) $F$ 对其第一个变量 $x + y$ 的偏导数，然后代入 $(x + y, xy)$。按上面的方法，使用：

1. $\displaystyle \frac{\partial u}{\partial x}$ 表示复合函数 $u(x, y)$ 对变量 $x$ 的偏导数:
   • $\displaystyle \frac{\partial u}{\partial x} = \frac{\partial F(x + y, x y)} {\partial x}$
2. $F'_1$ 表示 $F$ 对其第一个变量的偏导数:
   • $F'_1 = \displaystyle \frac{\partial F(x + y, x y)}{\partial (x + y)} = \displaystyle \frac{\partial u}{\partial (x + y)}$

全微分的一阶形式不变性

定理 若以 $x, y$ 为自变量的二元函数 $z = f(x, y)$ 可微，且 $z = f(x, y)$，$x = x(u, v)$，$y = y(u, v)$ 都具有连续偏导数，则复合函数 $z = f(x(u, v), y(u, v))$ 在点 $(u, v)$ 处具有连续偏导数（从而可微）并且有 $\displaystyle dz = \frac{\partial z}{\partial u} du + \frac{\partial z}{\partial v} dv$。

证明.

$$\begin{array}{ll} dz &= \displaystyle \frac{\partial z}{\partial x} dx + \frac{\partial z}{\partial y} dy \\ &= \displaystyle \frac{\partial z}{\partial x} \left( \frac{\partial x}{\partial u} du + \frac{\partial x}{\partial v} dv \right) + \frac{\partial z}{\partial y} \left( \frac{\partial y}{\partial u} du + \frac{\partial y}{\partial v} dv \right) \\ &= \displaystyle \left( \frac{\partial z}{\partial x} \frac{\partial x}{\partial u} + \frac{\partial z}{\partial y} \frac{\partial y}{\partial u} \right) du + \left( \frac{\partial z}{\partial x} \frac{\partial x}{\partial v} + \frac{\partial z}{\partial y} \frac{\partial y}{\partial v} \right) dv \\ &= \displaystyle \frac{\partial z}{\partial u} du + \frac{\partial z}{\partial v} dv \end{array}$$

这指出求微分对任何的 $(\triangle, \square)$ 都能得到相同形式的结果，无论 $\begin{cases}\triangle = x \\ \square = y\end{cases}$ 还是多么复杂的表达式。

$$d\ (\text{expr}) = \frac{\partial}{\partial \triangle}(\text{expr}) d\triangle + \frac{\partial}{\partial \square}(\text{expr}) d\square$$

这也是可以对一个等式两边求全微分的依据。

隐函数求导法则

由单个方程确定的隐函数

方程 $F(x, y, z) = 0$ 确定隐函数 $z = z(x, y)$ $\Leftrightarrow$ $F(x, y, z(x, y)) \equiv 0$。

定理 设函数 $F(x, y, z)$ 在点 $P_0(x_0, y_0, z_0)$ 的某个邻域内存在连续偏导数， 且 $F(x_0, y_0, z_0) = 0$，$F'_z(x_0, y_0, z_0) \neq 0$，那么方程 $F(x, y, z) = 0$ 在点 $P_0(x_0, y_0, z_0)$ 的某个邻域内始终能够唯一确定隐函数 $z = f(x, y)$，且这个隐函数具有连续偏导数，满足 $z_0 = f(x_0, y_0)$ 以及 $\displaystyle \frac{\partial z}{\partial x} = -\frac{F'_x}{F'_z}$、$\displaystyle \frac{\partial z}{\partial y} = -\frac{F'_y}{F'_z}$。（隐函数存在定理）

证明.

对 $F(x, y, z(x, y)) \equiv 0$ 两边对 $x$ 求偏导数，应用复合函数的求导法则，有 $\displaystyle F'_x \frac{\partial x}{\partial x} + F'_z \frac{\partial z}{\partial x} = 0$，因而 $\displaystyle \frac{\partial z}{\partial x} = -\frac{F'_x}{F'_z}$。这里 $F'_z$ 能够放在分母的位置是由于在 $P_0$ 点连续函数 $F'_z(P_0) \neq 0$，这样就能够保证在 $P_0$ 点某邻域内 $F'_z$ 不为 $0$。

对 $y$ 同理，有 $\displaystyle \frac{\partial z}{\partial y} = -\frac{F'_y}{F'_z}$。

偏导数 $\displaystyle \frac{\partial z}{\partial x}$、$\displaystyle \frac{\partial z}{\partial y}$ 在 $P_0$ 点连续是因为连续函数的四则运算结果仍然是连续函数。$\blacksquare$

实际的应用中，求解隐函数的偏导数时，通常也是直接对方程两边求偏导数，然后解方程。（或者也可以通过两边取全微分）

(*)由方程组确定的隐函数组

方程组 $\begin{cases}F(x, y, u, v) = 0 \\ G(x, y, u, v) = 0\end{cases}$ 确定隐函数组 $\begin{cases}u = u(x, y) \\ v = v(x, y)\end{cases}$ $\Leftrightarrow$ $\begin{cases}F(x, y, u(x, y), v(x, y)) \equiv 0 \\ G(x, y, u(x, y), v(x, y)) \equiv 0\end{cases}$。

定理 设函数 $F(x, y, u, v)$，$G(x, y, u, v)$ 在点 $P_0(x_0, y_0, u_0, v_0)$ 的某个邻域内存在连续偏导数， 且 $\begin{cases}F(x_0, y_0, u_0, v_0) = 0 \\ G(x_0, y_0, u_0, v_0) = 0\end{cases}$，并且二阶雅可比行列式 $\displaystyle J = \frac{\partial (F, G)}{\partial (u, v)} = \begin{vmatrix} \frac{\partial F}{\partial u} & \frac{\partial F}{\partial v} \\ \frac{\partial G}{\partial u} & \frac{\partial G}{\partial v} \end{vmatrix} \neq 0$，那么方程组 $\begin{cases}F(x, y, u, v) = 0 \\ G(x, y, u, v) = 0\end{cases}$ 在点 $P_0(x_0, y_0, u_0, v_0)$ 的某个邻域内始终能够唯一确定隐函数组 $\begin{cases}u = u(x, y) \\ v = v(x, y)\end{cases}$，且它们具有连续偏导数，满足 $\begin{cases}u_0 = u(x_0, y_0) \\ v_0 = v(x_0, y_0)\end{cases}$ 以及

$$\begin{array}{cc} \displaystyle \frac{\partial u}{\partial x} = -\frac{\frac{\partial (F, G)}{\partial (x, v)}}{\frac{\partial (F, G)}{\partial (u, v)}} & \displaystyle \frac{\partial u}{\partial y} = -\frac{\frac{\partial (F, G)}{\partial (y, v)}}{\frac{\partial (F, G)}{\partial (u, v)}} \\ \displaystyle \frac{\partial v}{\partial x} = -\frac{\frac{\partial (F, G)}{\partial (u, x)}}{\frac{\partial (F, G)}{\partial (u, v)}} & \displaystyle \frac{\partial v}{\partial y} = -\frac{\frac{\partial (F, G)}{\partial (u, y)}}{\frac{\partial (F, G)}{\partial (u, v)}} \end{array}$$

证明. 对方程组两边同时对 $x$ 求偏导数，有

$$\begin{cases} \displaystyle \frac{\partial F}{\partial x} + \frac{\partial F}{\partial u} \frac{\partial u}{\partial x} + \frac{\partial F}{\partial v} \frac{\partial v}{\partial x} = 0 \\ \displaystyle \frac{\partial G}{\partial x} + \frac{\partial G}{\partial u} \frac{\partial u}{\partial x} + \frac{\partial G}{\partial v} \frac{\partial v}{\partial x} = 0 \end{cases}$$

整理可得

$$\begin{bmatrix} \displaystyle \frac{\partial F}{\partial u} \\ \displaystyle \frac{\partial G}{\partial u} \end{bmatrix} \frac{\partial u}{\partial x} + \begin{bmatrix} \displaystyle \frac{\partial F}{\partial v} \\ \displaystyle \frac{\partial G}{\partial v} \end{bmatrix} \frac{\partial v}{\partial x} =- \begin{bmatrix} \displaystyle \frac{\partial F}{\partial x} \\ \displaystyle \frac{\partial G}{\partial x} \end{bmatrix}$$

运用克莱姆法则解关于 $\displaystyle (\frac{\partial u}{\partial x}, \frac{\partial v}{\partial x})$ 的线性方程组，有：

$$\begin{cases} \displaystyle \frac{\partial u}{\partial x} = \frac{-\begin{vmatrix}\frac{\partial F}{\partial x} & \frac{\partial F}{\partial v} \\ \frac{\partial G}{\partial x} & \frac{\partial G}{\partial v}\end{vmatrix}}{\quad \begin{vmatrix}\frac{\partial F}{\partial u} & \frac{\partial F}{\partial v} \\ \frac{\partial G}{\partial u} & \frac{\partial G}{\partial v}\end{vmatrix}} = -\frac{\displaystyle \frac{\partial(F, G)}{\partial (x, v)}}{\displaystyle \frac{\partial(F, G)}{\partial (u, v)}} \\ \\ \displaystyle \frac{\partial v}{\partial x} = \frac{-\begin{vmatrix}\frac{\partial F}{\partial u} & \frac{\partial F}{\partial x} \\ \frac{\partial G}{\partial u} & \frac{\partial G}{\partial x}\end{vmatrix}}{\quad \begin{vmatrix}\frac{\partial F}{\partial u} & \frac{\partial F}{\partial v} \\ \frac{\partial G}{\partial u} & \frac{\partial G}{\partial v}\end{vmatrix}} = -\frac{\displaystyle \frac{\partial(F, G)}{\partial (u, x)}}{\displaystyle \frac{\partial(F, G)}{\partial (u, v)}} \end{cases}$$

对 $y$ 求偏导的情况类似；有关解的存在性的证明、连续性的证明与由单个方程确定的隐函数类似。$\blacksquare$

(*)场的方向导数与梯度

数量场的方向导数

设数量场 $u(x, y, z)$ 在点 $P_0(x_0, y_0, z_0)$ 的某邻域 $U(P_0) \subset \mathbb{R}^3$ 有定义，$\overrightarrow{l}$ 是与 $x$ 轴正向夹角为 $\alpha$，与 $y$ 轴正向夹角为 $\beta$，与 $z$ 轴正向夹角为 $\gamma$ 的单位向量，$P(x, y, z)$ 是 $U(P_0)$ 内满足 $\overrightarrow{P_0 P} = \lambda \overrightarrow{l}$ （$\lambda > 0$）的任意一点，那么称

$$\lim_{\lambda \rightarrow 0} \frac{u(P) - u(P_0)}{\lambda} = \lim_{\lambda \rightarrow 0} \frac{\Delta_{\mathbf{l}}u}{\lambda}$$

为数量场 $u(x, y, z)$ 在点 $P_0$ 沿方向 $\overrightarrow{l}$ 的方向导数，记作 $\displaystyle \frac{\partial u}{\partial l}\Bigg|_{P_0}$。

可微 $\Rightarrow$ 任意方向的方向导数存在，有以下定理：

定理 若函数 $u(x, y, z)$ 在点 $P_0(x_0, y_0, z_0)$ 可微，则函数 $u(x, y, z)$ 在点 $P_0$ 沿任意方向 $\overrightarrow{l}$ 的方向导数存在，且有

$$\frac{\partial u}{\partial l}\Bigg|_{P_0} = \frac{\partial u}{\partial x}\Bigg|_{P_0} \cos \alpha + \frac{\partial u}{\partial y}\Bigg|_{P_0} \cos \beta + \frac{\partial u}{\partial z}\Bigg|_{P_0} \cos \gamma$$

其中 $\alpha$，$\beta$，$\gamma$ 分别是 $\overrightarrow{l}$ 与 $x$，$y$，$z$ 轴正向的夹角（即 $\displaystyle \frac{\overrightarrow{l}}{|\overrightarrow{l}|} = (\cos \alpha, \cos \beta, \cos \gamma)$）。

证明.

由于函数 $u(x, y, z)$ 在点 $P_0$ 可微，因此对于 $U(P_0)$ 内满足 $\overrightarrow{P_0 P} = \lambda \overrightarrow{l}$ （$\lambda > 0$）的任意一点 $P(x, y, z)$，都有

$$\begin{cases} \displaystyle u(P) - u(P_0) = u(x_0 + \Delta x, y_0 + \Delta y, z_0 + \Delta z) - u(x_0, y_0, z_0) = \Delta u \\ \displaystyle \Delta u = \frac{\partial u}{\partial x}\Bigg|_{P_0} \Delta x + \frac{\partial u}{\partial y}\Bigg|_{P_0} \Delta y + \frac{\partial u}{\partial z}\Bigg|_{P_0} \Delta z + \omicron(\sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2}) \\ \displaystyle \frac{\Delta x}{\sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2}} = \cos \alpha \\ \displaystyle \frac{\Delta y}{\sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2}} = \cos \beta \\ \displaystyle \frac{\Delta z}{\sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2}} = \cos \gamma \end{cases}$$

因此

$$\lim_{\substack{\Delta x \rightarrow 0 \\ \Delta y \rightarrow 0 \\ \Delta z \rightarrow 0}} \frac{\Delta u}{\sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2}} = \frac{\partial u}{\partial x}\Bigg|_{P_0} \cos \alpha + \frac{\partial u}{\partial y}\Bigg|_{P_0} \cos \beta + \frac{\partial u}{\partial z}\Bigg|_{P_0} \cos \gamma$$

由于当 $\Delta x \rightarrow 0$，$\Delta y \rightarrow 0$，$\Delta z \rightarrow 0$ 时，$\lambda \rightarrow 0$，因此有

$$\begin{array}{rl} \displaystyle \frac{\partial u}{\partial l}\Bigg|_{P_0} &= \displaystyle \lim_{\lambda \rightarrow 0} \frac{\Delta u}{\lambda} \\ &= \displaystyle \lim_{\substack{\Delta x \rightarrow 0 \\ \Delta y \rightarrow 0 \\ \Delta z \rightarrow 0}} \frac{\Delta u}{\sqrt{(\Delta x)^2 + (\Delta y)^2 + (\Delta z)^2}} \\ &= \displaystyle \frac{\partial u}{\partial x}\Bigg|_{P_0} \cos \alpha + \frac{\partial u}{\partial y}\Bigg|_{P_0} \cos \beta + \frac{\partial u}{\partial z}\Bigg|_{P_0} \cos \gamma \qquad \blacksquare \end{array}$$

任意方向方向导数存在 $\nRightarrow$ 连续；任意方向方向导数存在 $\nRightarrow$ 可微，例如函数 $u(x, y) = \begin{cases}\displaystyle 1, & 0 < x < y^2 \\0, & \text{otherwise}\end{cases}$，在点 $(0, 0)$ 处不连续，不可微，但在点 $(0, 0)$ 处沿任意方向的方向导数都存在。

取路径上任意一点都满足 $0 < x < y^2$ 的路径，$\displaystyle \lim_{(x, y) \rightarrow (0, 0)} u(x, y) = 1$；取路径上任意一点都不满足 $0 < x < y^2$ 的路径，$\displaystyle \lim_{(x, y) \rightarrow (0, 0)} u(x, y) = 0$。从而极限不存在，从而函数在点 $(0, 0)$ 处不连续。因此函数在 $(0, 0)$ 处不可微。

而函数 $u(x, y)$ 在 $(0, 0)$ 处沿着任意方向的方向导数 $\displaystyle \lim_{\lambda \rightarrow 0} \frac{u(\lambda \cos \alpha, \lambda \sin \alpha) - u(0, 0)}{\lambda} = \lim_{\lambda \rightarrow 0} \frac{0 - 0}{\lambda} = 0$。

Note

考虑 $x = \lambda \cos \alpha > 0$ 时，总是可以取 $\lambda$ 足够小，使得 $\displaystyle \lambda < \frac{\cos \alpha}{\sin^2 \alpha}$（由于 $\lambda$ 和 $\alpha$ 相互独立，而 $\alpha$ 是确定的），从而 $\lambda \cos \alpha > (\lambda \sin \alpha)^2$，从而 $u(\lambda \cos \alpha, \lambda \sin \alpha) = 0$。

Note

此处不能使用偏导数均存在来论证函数沿各方向的方向导数存在。

任意方向方向导数存在 $\nRightarrow$ 偏导数均存在。例如函数 $u(x, y) = \sqrt{x^2 + y^2}$，该函数在 $(0, 0)$ 处的偏导数均不存在，但函数在 $(0, 0)$ 处沿任意方向的方向导数都存在：$\displaystyle \lim_{\lambda \rightarrow 0} \frac{u(\lambda \cos \alpha, \lambda \sin \alpha) - u(0, 0)}{\lambda} = \lim_{\lambda \rightarrow 0} \frac{\lambda}{\lambda} = 1$。

Note

对于不可微的函数，不一定满足 $\displaystyle \frac{\partial u}{\partial l}\Bigg|_{P_0} = \displaystyle \frac{\partial u}{\partial x}\Bigg|_{P_0} \cos \alpha + \frac{\partial u}{\partial y}\Bigg|_{P_0} \cos \beta$。这是为什么这个函数在 $(0, 0)$ 处任意方向的方向导数都存在，但偏导数不存在的原因。

在几何意义上，沿 $x$ 轴正方向的方向导数和函数对 $x$ 的偏导数也是不同的。前者只要求从一个方向逼近时的切线斜率（单侧极限），而后者要求两个方向逼近时的切线斜率都要相同（左右极限相同）。

各个偏导数均存在 $\nRightarrow$ 所有方向导数存在。例如函数 $u(x, y) = \begin{cases}\displaystyle 1, & x\cdot y = 0 \\0, & \text{otherwise}\end{cases}$，在点 $(0, 0)$ 处所有偏导数均存在，但函数在 $(0, 0)$ 处沿不平行于任意坐标轴的方向的方向导数不存在。

数量场的梯度

$$\begin{array}{ll} \displaystyle \frac{\partial u}{\partial l}\Bigg|_{P_0} &= \displaystyle \frac{\partial u}{\partial x}\Bigg|_{P_0} \cos \alpha + \frac{\partial u}{\partial y}\Bigg|_{P_0} \cos \beta + \frac{\partial u}{\partial z}\Bigg|_{P_0} \cos \gamma \\ &= \displaystyle \left( \frac{\partial u}{\partial x}\Bigg|_{P_0}, \frac{\partial u}{\partial y}\Bigg|_{P_0}, \frac{\partial u}{\partial z}\Bigg|_{P_0} \right) \cdot \left( \cos \alpha, \cos \beta, \cos \gamma \right) \\ &= \displaystyle \left( \frac{\partial u}{\partial x}, \frac{\partial u}{\partial y}, \frac{\partial u}{\partial z} \right)\Bigg|_{P_0} \cdot \left( \cos \alpha, \cos \beta, \cos \gamma \right) \end{array}$$

定义 $\displaystyle \nabla u := \left( \frac{\partial u}{\partial x}, \frac{\partial u}{\partial y}, \frac{\partial u}{\partial z} \right)$ 为函数 $u(x, y, z)$ 的梯度（函数），$\nabla u(P_0)$ 为函数 $u(x, y, z)$ 在点 $P_0$ 处的梯度（值）。从而 $\displaystyle \frac{\partial u}{\partial l}\Bigg|_{P_0} = \nabla u(P_0) \cdot \overrightarrow{e}_l$，其中 $\overrightarrow{e}_l = (\cos \alpha, \cos \beta, \cos \gamma)$ 是与 $\overrightarrow{l}$ 同方向的单位向量。

由 $\displaystyle \frac{\partial u}{\partial l}\Bigg|_{P_0} = \nabla u(P_0) \cdot \overrightarrow{e}_l = |\nabla u(P_0)| \cos \theta$，其中 $\theta$ 是 $\nabla u(P_0)$ 与 $\overrightarrow{l}$ 的夹角，知 $\nabla u(P_0)$ 的方向是函数 $u(x, y, z)$ 在点 $P_0$ 处方向导数最大的方向（此时 $\cos \theta = 1$），该方向导数的值为 $|\nabla u(P_0)|$。

多元函数的泰勒公式

定理 若函数 $u = f(x, y)$ 在点 $P_0(x_0, y_0)$ 的某邻域 $U(P_0)$ 内具有 $n + 1$ 阶连续偏导数，则有（多元函数的泰勒定理）

$$\begin{array}{rl} \displaystyle f(x_0 + h, y_0 + k) &= \displaystyle f(x_0, y_0) + \left(h \frac{\partial}{\partial x} + k\frac{\partial}{\partial y} \right)f(x_0, y_0) \\ &+ \displaystyle \frac{1}{2!} \left(h \frac{\partial}{\partial x} + k\frac{\partial}{\partial y} \right)^2 f(x_0, y_0) \\ &+ \displaystyle \frac{1}{3!} \left(h \frac{\partial}{\partial x} + k\frac{\partial}{\partial y} \right)^3 f(x_0, y_0) + \cdots \\ &+ \displaystyle \frac{1}{n!} \left(h \frac{\partial}{\partial x} + k\frac{\partial}{\partial y} \right)^n f(x_0, y_0) \\ &+ \displaystyle \frac{1}{(n + 1)!} \left(h \frac{\partial}{\partial x} + k\frac{\partial}{\partial y} \right)^{n + 1} f(x_0 + \theta h, y_0 + \theta k) \end{array}$$

其中，$\theta \in (0, 1)$，$\displaystyle \left(h \frac{\partial}{\partial x} + k\frac{\partial}{\partial y} \right)^n$ 按多项式展开，例如 $\displaystyle \left(h \frac{\partial}{\partial x} + k\frac{\partial}{\partial y} \right)^2 = h^2 \frac{\partial^2}{\partial x^2} + 2hk \frac{\partial^2}{\partial x \partial y} + k^2 \frac{\partial^2}{\partial y^2}$（连续的混合偏导数可以交换求偏导的顺序）。

证明.

设 $\psi(t) = f(x_0 + th, y_0 + tk)$，则 $\psi(0) = f(x_0, y_0)$，$\psi(1) = f(x_0 + h, y_0 + k)$。

$$\begin{array}{lcl} \psi'(t) =& \displaystyle \frac{d}{dt} f(x_0 + th, y_0 + tk) &= \displaystyle \left(h \frac{\partial}{\partial x} + k \frac{\partial}{\partial y}\right)f(x_0 + th, y_0 + tk) \\ \psi''(t) =& \dots &= \displaystyle \left(h \frac{\partial}{\partial x} + k \frac{\partial}{\partial y}\right)^2 f(x_0 + th, y_0 + tk) \\ \psi^{(n)}(t) =& \dots &= \displaystyle \left(h \frac{\partial}{\partial x} + k \frac{\partial}{\partial y}\right)^n f(x_0 + th, y_0 + tk) \\ \end{array}$$

由一元函数的泰勒定理，存在 $\theta \in (0, 1)$，使得

$$\begin{array}{ll} \displaystyle \psi(1) &= \displaystyle \psi(0) + \frac{1}{1!} \psi'(0)\cdot(1 - 0)^1 + \frac{1}{2!} \psi''(0)\cdot(1 - 0)^2 + \cdots + \frac{1}{n!} \psi^{(n)}(0)\cdot(1 - 0)^n + \frac{1}{(n + 1)!} \psi^{(n + 1)}(\theta) \cdot (1 - 0)^{n + 1} \\ &= \displaystyle \psi(0) + \frac{1}{1!} \psi'(0) + \frac{1}{2!} \psi''(0) + \cdots + \frac{1}{n!} \psi^{(n)}(0) + \frac{1}{(n + 1)!} \psi^{(n + 1)}(\theta) \end{array}$$

将上述 $\psi(t)^{(m)}$ 全部代入一元函数的泰勒定理，即得

$$\begin{array}{rl} \displaystyle f(x_0 + h, y_0 + k) &= \displaystyle f(x_0, y_0) + \left(h \frac{\partial}{\partial x} + k\frac{\partial}{\partial y} \right)f(x_0, y_0) \\ &+ \displaystyle \frac{1}{2!} \left(h \frac{\partial}{\partial x} + k\frac{\partial}{\partial y} \right)^2 f(x_0, y_0) + \cdots \\ &+ \displaystyle \frac{1}{n!} \left(h \frac{\partial}{\partial x} + k\frac{\partial}{\partial y} \right)^n f(x_0, y_0) \\ &+ \displaystyle \frac{1}{(n + 1)!} \left(h \frac{\partial}{\partial x} + k\frac{\partial}{\partial y} \right)^{n + 1} f(x_0 + \theta h, y_0 + \theta k) \quad \blacksquare \end{array}$$

令 $n = 0$，即可得到二元函数的拉格朗日中值定理：

$$f(x_0 + h, y_0 + k) - f(x_0, y_0) = h f'_x(x_0 + \theta h, y_0 + \theta k) + k f'_y(x_0 + \theta h, y_0 + \theta k)$$

其中 $\theta \in (0, 1)$。可以用此定理证明一个二元函数在某个区域 $G$ 内是否是仅关于 $x$ 或 $y$ 或常值的函数。

多元函数的极值与最值

多元函数的无条件极值

定义 设函数 $z = f(x, y)$ 在点 $P_0(x_0, y_0)$ 的某邻域 $U(P_0)$ 内有定义，如果对于 $U(P_0)$ 内任意点 $(x, y)$，都有 $f(x, y) \leq f(x_0, y_0)$，则称 $f(x_0, y_0)$ 是函数 $f(x, y)$ 在点 $P_0$ 的一个极大值；如果对于 $U(P_0)$ 内任意点 $(x, y)$，都有 $f(x, y) \geq f(x_0, y_0)$，则称 $f(x_0, y_0)$ 是函数 $f(x, y)$ 在点 $P_0$ 的一个极小值。极大值和极小值统称为极值。取极大值和极小值的点称为极值点。

定理 如果函数 $z = f(x, y)$ 在点 $P_0(x_0, y_0)$ 存在偏导数，且在点 $P_0$ 取得极值，那么 $f'_x(x_0, y_0) = 0$，$f'_y(x_0, y_0) = 0$。（极值的必要条件，满足条件 $f'_x(x_0, y_0) = 0$，$f'_y(x_0, y_0) = 0$ 的点被称为 驻点）

证明. 证明极大值的情况，极小值类似：

根据定义，存在某邻域 $U(P_0)$，使得对于 $U(P_0)$ 内任意点 $(x, y)$，都有 $f(x, y) \leq f(x_0, y_0)$。由于偏导数 $f'_x(x_0, y_0)$ 存在，假设偏导数的值为 $A \neq 0$，对于任意给定正数 $\varepsilon$，不妨令其为 $|A|$，都应当存在 $\delta > 0$，使得当 $0 < |\Delta x| < \delta$ 时，有

$$\begin{array}{cc} \displaystyle \left| \frac{f(x_0 + \Delta x, y_0) - f(x_0, y_0)}{\Delta x} - A \right| \leq \varepsilon \\ \displaystyle A - |A| \leq \frac{f(x_0 + \Delta x, y_0) - f(x_0, y_0)}{\Delta x} \leq A + |A| \\ \displaystyle \frac{A - |A|}{f(x_0 + \Delta x, y_0) - f(x_0, y_0)} \leq \frac{1}{\Delta x} \leq \frac{A + |A|}{f(x_0 + \Delta x, y_0) - f(x_0, y_0)} \end{array}$$

这是不可能满足的，因为这个不等式要求当 $0 < |\Delta x| < \delta$ 时，$\displaystyle \frac{1}{\Delta x}$ 非负（或者非正，取决于具体的 $A$）. 因此 $A = 0$，即 $f'_x(x_0, y_0) = 0$。同理可证 $f'_y(x_0, y_0) = 0$。$\blacksquare$

定理 设函数 $z = f(x, y)$ 在点 $P_0(x_0, y_0)$ 的某邻域 $U(P_0)$ 内连续、且具有二阶连续偏导数，如果有 $f_{x}(x_0, y_0) = 0$，$f_{y}(x_0, y_0) = 0$，并且 $A = f''_{xx}(x_0, y_0)$，$B = f''_{xy}(x_0, y_0)$，$C = f''_{yy}(x_0, y_0)$ 满足：（极值的充分条件）

• $\begin{vmatrix} A & B \\ B & C \end{vmatrix} > 0$，则点 $P_0$ 是函数 $f(x, y)$ 的极值点，且是极大值点或极小值点，取决于 $A$ 的正负性（或 $C$ 的正负性，这两项在这个条件下必然同号）：
• 若 $A > 0$，则 $P_0$ 是极小值点；
• 若 $A < 0$，则 $P_0$ 是极大值点；
• $\begin{vmatrix} A & B \\ B & C \end{vmatrix} < 0$，则点 $P_0$ 不是函数 $f(x, y)$ 的极值点；
• $\begin{vmatrix} A & B \\ B & C \end{vmatrix} = 0$，不能断定点 $P_0$ 是否是函数 $f(x, y)$ 的极值点。

证明. 泰勒展开至 $2$ 阶导数，对 $U(P_0)$ 内任意的点 $P(x_0 + h, y_0 + k)$，存在 $\theta \in (0, 1)$，使得

$$\begin{array}{rl} \displaystyle f(x_0 + h, y_0 + k) &= \displaystyle f(x_0, y_0) + \left(h \frac{\partial}{\partial x} + k\frac{\partial}{\partial y} \right)f(x_0, y_0) \\ &+ \displaystyle \frac{1}{2!} \left(h \frac{\partial}{\partial x} + k\frac{\partial}{\partial y} \right)^2 f(x_0 + \theta h, y_0 + \theta k) \\ &= \displaystyle f(x_0, y_0) + \frac{1}{2!} \left(h \frac{\partial}{\partial x} + k\frac{\partial}{\partial y} \right)^2 f(x_0 + \theta h, y_0 + \theta k) \end{array}$$

当 $h \to 0$，$k \to 0$ 时，有 $x_0 + \theta h \to x_0$，$y_0 + \theta k \to y_0$，由于 $f(x, y)$ 在点 $P_0$ 处连续，因此有 $f(x_0 + \theta h, y_0 + \theta k) \to f(x_0, y_0)$。此时有

$$\begin{array}{rl} f(x_0 + h, y_0 + k) - f(x_0, y_0) &\sim \displaystyle \frac{1}{2!} \left(h \frac{\partial}{\partial x} + k\frac{\partial}{\partial y} \right)^2 f(x_0, y_0) \\ &= \displaystyle \frac{1}{2!} (h^2 f''_{xx}(x_0, y_0) + 2hk f''_{xy}(x_0, y_0) + k^2 f''_{yy}(x_0, y_0)) \\ &= \displaystyle (A h^2 + 2Bhk + Ck^2) \\ &= \begin{bmatrix} h & k \end{bmatrix} \begin{bmatrix} A & B \\ B & C \end{bmatrix} \begin{bmatrix} h \\ k \end{bmatrix} \end{array}$$

根据极限的保号性和二次型的正定性，可以得到结论：

(1) 当二次型矩阵 $\begin{bmatrix} A & B \\ B & C \end{bmatrix}$ 顺序主子式 $\begin{vmatrix} A \end{vmatrix}$、$\begin{vmatrix} A & B \\ B & C \end{vmatrix}$ 均大于 $0$，即 $A > 0$ 并且 $AC - B^2 > 0$，该二次型正定，从而 $f(x_0 + h, y_0 + k) - f(x_0, y_0) > 0$，$P_0$ 是极小值点；

(2) 当二次型矩阵 $\begin{bmatrix} A & B \\ B & C \end{bmatrix}$ 顺序主子式 $\begin{vmatrix} A \end{vmatrix}$、$\begin{vmatrix} A & B \\ B & C \end{vmatrix}$ 与 $(-1)^k$ 同号，即 $A < 0$ 并且 $AC - B^2 > 0$，该二次型负定，从而 $f(x_0 + h, y_0 + k) - f(x_0, y_0) < 0$，$P_0$ 是极大值点；

(3) 当 $\begin{vmatrix} A & B \\ B & C \end{vmatrix} < 0$ ，二次型矩阵 $\begin{bmatrix} A & B \\ B & C \end{bmatrix}$ 的特征值 $\lambda_1 \lambda_2 = AC - B^2 < 0$。由于实对称矩阵总是可以使用正交矩阵对角化，有 $\begin{bmatrix} A & B \\ B & C \end{bmatrix} \overset{T}{\sim} \begin{bmatrix} \lambda_1 & 0 \\ 0 & \lambda 2 \end{bmatrix}$，从而二次型不定，$f(x_0 + h, y_0 + k) - f(x_0, y_0)$ 的符号与 $h$，$k$ 的取值有关，$P_0$ 不是极值点；

(4) 当 $\begin{vmatrix} A & B \\ B & C \end{vmatrix} = 0$，由于实对称矩阵总是可以使用正交矩阵对角化，有 $\begin{bmatrix} A & B \\ B & C \end{bmatrix} \overset{T}{\sim} \begin{bmatrix} \text{tr} \left(\scriptscriptstyle \begin{bmatrix} A & B \\ B & C \end{bmatrix} \right) & 0 \\ 0 & 0 \end{bmatrix}$，二次型的正定性与二次型矩阵的迹有关，凭此可判断 $P_0$ 是极小值点（二次型正定）还是极大值点（二次型负定）。$\blacksquare$

Note

这里的矩阵 $\begin{bmatrix} A & B \\ B & C \end{bmatrix}$ 的名字叫做 Hessian 矩阵。结论可以推广至有限的 $n$ 维形式。

多元函数的条件最值（拉格朗日乘数法）

当 $f$ 和 $G$ 都有连续偏导数时，求解 $f(x, y, z)$ 在约束条件 $G(x, y, z) = 0$ 下的极值点 $(x_0, y_0, z_0)$，可以转化为求解方程组 $\begin{cases}f'_x + \lambda G'_x = 0 \\ f'_y + \lambda G'_y = 0 \\ f'_z + \lambda G'_z = 0 \\ G = 0\end{cases}$ 的解。

这个方程组的解是函数 $L(x, y, z, \lambda) = f(x, y, z) + \lambda G(x, y, z)$ 取得极值的必要条件。这个方法称为拉格朗日乘数法。

证明. 由于 $G$ 具有连续偏导数，因此 $G(x, y, z) = 0$ 唯一确定隐函数 $z = z(x, y)$，从而问题转化为求解 $u = f(x, y, z(x, y))$ 的无条件极值。

$u = f(x, y, z(x, y))$ 在点 $(x_0, y_0)$ 处取得极值的必要条件是 $u'_x(x_0, y_0) = 0$，$u'_y(x_0, y_0) = 0$。由链式法则以及隐函数求导法，有

$$\begin{cases} \displaystyle u'_x = f'_x + f'_z z'_x = f'_x - \frac{G'_x}{G'_z} f'_z = 0 \\ \displaystyle u'_y = f'_y + f'_z z'_y = f'_y - \frac{G'_y}{G'_z} f'_z = 0 \end{cases}$$

从而 $\begin{cases}\displaystyle \frac{f'_x}{G'_x} = \frac{f'_z}{G'_z} \\\displaystyle \frac{f'_y}{G'_y} = \frac{f'_z}{G'_z}\end{cases}$，即 $\displaystyle \frac{f'_x}{G'_x} = \frac{f'_y}{G'_y} = \frac{f'_z}{G'_z} = -\lambda$。

这等价于 $\begin{cases}f'_x + \lambda G'_x = 0 \\ f'_y + \lambda G'_y = 0 \\ f'_z + \lambda G'_z = 0\end{cases}$。$\blacksquare$

Question

$G'_z(x_0, y_0, z_0) \neq 0$ ？

使用拉格朗日乘数法可以求解在给定约束 $G(x, y, z) = 0$ 下的所有可能极值点（由于是必要条件）。因此，只需要比较在这些点上函数 $f(x, y, z)$ 的值，就可以得到函数 $f(x, y, z)$ 在约束 $G(x, y, z) = 0$ 下的最值。

偏导数在几何上的应用

---

1. 苏德矿《微积分》下册 P.53 ↩