一元函数的反常积分

本文详细介绍了一元函数的反常积分及其应用。主要内容包括：

无穷区间上的反常积分（第一类反常积分）：定义了反常积分的概念，阐述了其计算方法。
无界函数的反常积分（第二类反常积分）：讨论了在有瑕点的情况下，如何计算反常积分。
柯西主值：引入了柯西主值的概念，解释了其在处理特殊反常积分时的重要性。
p积分的敛散性：分析了第一类和第二类 p 积分的收敛性判别方法，总结了 p 值对积分敛散性的影响。
反常积分的敛散性判别法：介绍了比较判别法（包括极限形式）和绝对收敛准则，提供了判断反常积分是否收敛的实用工具。
Gamma 函数：定义了 Gamma 函数，讨论了其收敛性、递推公式以及解析延拓。

通过本文的学习，读者可以全面掌握一元函数反常积分的理论基础和计算技巧，为深入研究高等数学奠定坚实的基础。

（摘要由 OpenAI o1-preview 生成）

无穷区间上的反常积分（第一类反常积分）¶

设函数 \(f(x)\) 在区间 \([a, +\infty)\) 连续，于是 \(\forall t > a\)，\(\displaystyle \int_a^t f(x) dx\) 存在，称下面的极限是函数 \(f(x)\) 在区间 \([a, +\infty)\) 上的反常积分：

\[ \int_a^{+\infty} f(x) dx ::= \lim_{t \rightarrow +\infty} \int_a^t f(x) dx \]

类似地，我们定义函数 \(f(x)\) 在区间 \((-\infty, b]\) 上的反常积分：

\[ \int_{-\infty}^b f(x) dx ::= \lim_{t \rightarrow -\infty} \int_t^b f(x) dx \]

而对于区间 \((-\infty, +\infty)\)，由于这个积分区间实际上隐藏了两个极限的过程，定义函数 \(f(x)\) 在区间 \((-\infty, +\infty)\) 上的反常积分为：

\[ \int_{-\infty}^{+\infty} f(x) dx ::= \lim_{t \rightarrow -\infty} \int_t^c f(x) dx + \lim_{t \rightarrow +\infty} \int_c^t f(x) dx \]

当且仅当等式右边两个极限均收敛，反常积分收敛。

无界函数的反常积分（第二类反常积分）¶

设函数 \(f(x)\) 在区间 \((a, b]\) 连续，\(\displaystyle \lim_{x \rightarrow a^+} f(x) = \infty\)（此时称 \(a\) 为瑕点），于是 \(\forall \varepsilon \in (0, b - a)\)，\(\displaystyle \int_{a + \varepsilon}^b f(x) dx\) 存在，称下面的极限是函数 \(f(x)\) 在区间 \((a, b]\) 上的反常积分：

\[ \int_a^b f(x) dx ::= \lim_{\varepsilon \rightarrow 0^+} \int_{a + \varepsilon}^b f(x) dx \]

类似地，我们定义函数 \(f(x)\) 在区间 \([a, b)\) 上的反常积分：

\[ \int_a^b f(x) dx ::= \lim_{\varepsilon \rightarrow 0^+} \int_{a}^{b - \varepsilon} f(x) dx \]

以及函数 \(f(x)\) 在区间 \([a, c) \cup (c, b]\) 上的反常积分：

\[ \int_a^b f(x) dx ::= \lim_{\varepsilon \rightarrow 0^+} \int_{a}^{c - \varepsilon} f(x) dx + \lim_{\varepsilon \rightarrow 0^+} \int_{c + \varepsilon}^b f(x) dx \]

由于只要 \(f(x)\) 是有界的，就一定有函数 \(\displaystyle F(x) = \int_0^x f(t) dt\) 是连续的，不存在瑕点的函数依然可以由上面的方法计算出其在某个区间上的第二类反常积分，该积分值等于其在对应闭区间上的定积分值。

柯西主值¶

在一些需要拆成两个（或多个，下略）极限计算的反常积分中（例如，\(\displaystyle \int_{-\infty}^{+\infty} f(x) dx\)；又例如瑕点位于区间内的第二类反常积分），拆分出的两个极限须分别处理，因为两极限式的收敛速度可能不同，当两个极限都收敛时，反常积分才收敛。

这也是奇函数在无穷区间 \((-\infty, +\infty)\) 的反常积分值不一定为 \(0\)、甚至不一定收敛的原因（对于 \(\{x' | -\infty < x' < 0\}\) 和 \(\{x | 0 < x < +\infty\}\)，可以建立 \(x' = -x\) 的映射，也可以建立 \(x' = -x^2\) 的映射）。

在柯西主值的理解下，假设这两个极限的收敛速度相同。例如：

\[ \text{p.v.} \int_{-\infty}^{+\infty} f(x) dx = \lim_{R \rightarrow +\infty} \int_{-R}^{R} f(x) dx \]

这样，奇函数在无穷区间 \((-\infty, +\infty)\) 的反常积分之柯西主值为 \(0\)。

在计算积分的柯西主值时，使用换元积分法可能会因为不同的换元策略而得到不同的柯西主值。

更多信息参见：柯西主值 - 维基百科，自由的百科全书

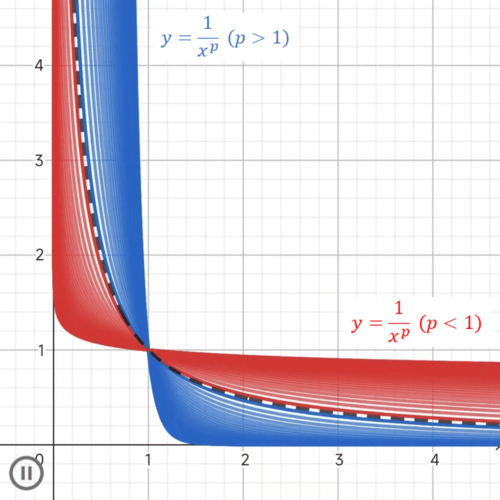
p积分¶

第一、第二p积分的敛散性结论可以借助图像记忆，其中，\(p\) 取值的分界点为 \(p = 1\)，在此处，p积分发散。

第一p反常积分 讨论 \(\displaystyle \int_a^{+\infty} \frac{1}{x^p} dx\) 的敛散性。

\(p = 1\) 时，

\[ \begin{array}{rl} \displaystyle I = \int_a^{+\infty} \frac{1}{x} dx &= \displaystyle \lim_{t \rightarrow +\infty} \int_a^t \frac{1}{x} dx \\ &= \displaystyle \lim_{t \rightarrow +\infty} \ln x \left|^t_a\right. \\ &= \displaystyle +\infty \end{array} \]

\(p \neq 1\) 时，

\[ \begin{array}{rl} \displaystyle I = \int_a^{+\infty} x^{-p} dx &= \displaystyle \lim_{t \rightarrow +\infty} \int_a^t x^{-p} dx \\ &= \displaystyle \lim_{t \rightarrow +\infty} \frac{x^{-p+1}}{-p+1} \left|^t_a\right. \\ &= \displaystyle \frac{1}{1-p} (\lim_{t \rightarrow +\infty} t^{1-p} - \lim_{t \rightarrow +\infty} a^{1-p}) \\ &= \left\{ \begin{array}{ll} \displaystyle -\frac{1}{1-p}a^{1-p} & (p > 1)\\ \displaystyle +\infty & (p < 1) \end{array} \right. \end{array} \]

综上所述，当 \(p > 1\)，反常积分 \(\displaystyle \int_a^{+\infty} \frac{1}{x^p} dx\) 收敛；当 \(p \leq 1\)，反常积分 \(\displaystyle \int_a^{+\infty} \frac{1}{x^p} dx\) 发散。

第二p反常积分 讨论 \(\displaystyle \int_a^b \frac{1}{(x - a)^p} dx\) 的敛散性。

令 \(x - a = t\)，\(dx = d(t + a) = dt\)，原积分转化为 \(\displaystyle \int_0^{b-a} \frac{1}{t^p} dt\)，下面讨论这个积分的敛散性。

\(p = 1\) 时，

\[ \begin{array}{rl} \displaystyle I = \int_0^{b-a} \frac{1}{t} dt &= \displaystyle \lim_{\varepsilon \rightarrow 0^+} \int_{0+\varepsilon}^{b-a} \frac{1}{t} dt \\ &= \displaystyle \lim_{\varepsilon \rightarrow 0^+} \ln t \left|_{0+\varepsilon}^{b-a}\right. \\ &= \displaystyle +\infty \end{array} \]

\(p \neq 1\) 时，

\[ \begin{array}{rl} \displaystyle I = \int_0^{b-a} t^{-p} dt &= \displaystyle \lim_{\varepsilon \rightarrow 0^+} \int_{0+\varepsilon}^{b-a} t^{-p} dt \\ &= \displaystyle \lim_{\varepsilon \rightarrow 0^+} \frac{t^{-p+1}}{-p+1} \left|_{0+\varepsilon}^{b-a}\right. \\ &= \displaystyle \frac{1}{1-p}\left( \lim_{\varepsilon \rightarrow 0^+} (b - a)^{-p+1} - \lim_{\varepsilon \rightarrow 0^+} \varepsilon^{-p+1} \right) \\ &= \left\{ \begin{array}{ll} \displaystyle +\infty & (p > 1)\\ \displaystyle \frac{1}{1-p}(b-a)^{1-p} & (p < 1) \end{array} \right. \end{array} \]

综上所述，当 \(p < 1\)，反常积分 \(\displaystyle \int_0^{b-a} \frac{1}{t^p} dt\) 收敛；当 \(p \geq 1\)，反常积分 \(\displaystyle \int_0^{b-a} \frac{1}{t^p} dt\) 发散。

反常积分的敛散性¶

使用极限形式的比较判别法，利用p积分的敛散性结论，可以将反常积分的敛散性问题转化为求极限的问题。

无穷区间上反常积分的敛散性判别法¶

比较判别法 设函数 \(f(x)\)， \(g(x)\) 在区间 \([a, +\infty)\) 连续，且有 \(0 \leq f(x) \leq g(x)\)，则：

若 \(\displaystyle \int_a^{+\infty} g(x) dx\) 收敛，\(\displaystyle \int_a^{+\infty} f(x) dx\) 收敛。即，大的收敛小的一定收敛。
若 \(\displaystyle \int_a^{+\infty} f(x) dx\) 发散，\(\displaystyle \int_a^{+\infty} g(x) dx\) 发散。即，小的发散大的一定发散。

利用不定积分收敛的定义及不等式的传递性即可证明。

比较判别法（极限形式） 设函数 \(f(x)\)， \(g(x)\) 在区间 \([a, +\infty)\) 非负连续，并且有 \(\displaystyle \lim_{x\rightarrow +\infty}\frac{f(x)}{g(x)} = \lambda\)，则：

若 \(\lambda > 0\)，\(\displaystyle \int_a^{+\infty} g(x) dx\) 与 \(\displaystyle \int_a^{+\infty} f(x) dx\) 同敛散。
若 \(\lambda = 0\)，分母是分子的高阶量，若 \(\displaystyle \int_a^{+\infty} g(x) dx\) 收敛，\(\displaystyle \int_a^{+\infty} f(x) dx\) 收敛。
若 \(\lambda = \infty\)，分子是分母的高阶量，若 \(\displaystyle \int_a^{+\infty} g(x) dx\) 发散，\(\displaystyle \int_a^{+\infty} f(x) dx\) 发散。

使用极限的定义，利用比较判别法即可证明。

绝对收敛准则 设函数 \(f(x)\) 在区间 \([a, +\infty)\) 连续，如果 \(\displaystyle \int_a^{+\infty} |f(x)| dx\) 收敛，则 \(\displaystyle \int_a^{+\infty} f(x) dx\) 收敛，此时称 \(\displaystyle \int_a^{+\infty} f(x) dx\) 绝对收敛。

证明. 由于 \(0 \leq f(x) + |f(x)| \leq 2|f(x)|\)，由比较判别法知 \(\displaystyle \int_a^{+\infty} \left( f(x) + |f(x)| \right) dx\) 收敛。又由于：

\[ \int_a^{+\infty} f(x) dx = \int_a^{+\infty} \left( f(x) + |f(x)| \right) dx - \int_a^{+\infty} |f(x)| dx \]

因此，\(\displaystyle \int_a^{+\infty} f(x) dx\) 收敛。

无界函数反常积分的敛散性判别法¶

所有结论与无穷区间上反常积分的敛散性判别法一致，有比较判别法、比较判别法（极限形式）、绝对收敛准则，极限过程 \(x\rightarrow +\infty\) 需要改为从对应方向趋近于瑕点 \(c\)，例如 \(x\rightarrow c^-\) 与 \(x\rightarrow c^+\)。

使用比较判别法的极限形式判断敛散性的一个方法¶

计算瑕点处 \(f(x)\) 与 \(\displaystyle \frac{1}{x^{1 + \varepsilon}}\) 的比值的极限，其中 \(\varepsilon\) 是一个微小扰动。

当用于判断已知的反常积分的敛散性时，问题转化为判断极限存在时 \(\varepsilon\) 的正负性，从而判断反常积分的敛散性。

当用于计算含参数的反常积分收敛或发散的条件时，问题转化为当 \(\varepsilon > 0\) 或 \(\varepsilon < 0\) 时（依据题目的具体情况而定），极限存在的条件。

这个方法可以用于判断已知的反常积分是否收敛，或是用于计算含参数的反常积分收敛或发散的条件。其优势在于这个方法与求极限的方法相同，利于理解而不需要额外的知识储备（相比直接使用等价无穷小的方法）。下面举两个例子说明。

【TODO】

(*) Gamma 函数¶

关于 \(s\) 的 Gamma 函数 \(\Gamma(s)\) 被下面的反常积分所定义：

\[ \Gamma(s) = \int_0^{+\infty} x^{s-1}e^{-x} dx \qquad (s > 0) \]

Gamma 函数的敛散性¶

\[ \Gamma(s) = \int_0^1 x^{s-1}e^{-x} dx + \int_1^{+\infty} x^{s-1}e^{-x} dx = I_1 + I_2 \]

\(I_1\) 是第二类反常积分，由于 \(x \rightarrow 0^+\) 时，

\[ x^{s-1}e^{-x} = x^{s-1}(e^{-x} - 1) + x^{s-1} \sim x^s + x^{s-1} = (x + 1) x^{s-1} \sim 1 \cdot x^{s-1} \]

（第一个等价无穷小可以代换是因为 \(\displaystyle \lim_{x\rightarrow 0^+} \frac{x^s}{x^{s - 1}} \neq -1\)，第二个等价无穷小是因为极限式中非零因子可以提出极限号先算）

因此，当 \(1 - s < 1\)，即 \(s > 0\)，\(I_1\) 收敛。

\(I_2\) 是第一类反常积分，由于 \(\displaystyle \lim_{x\rightarrow +\infty} \frac{x^k}{a^x} = 0\)（\(a > 1\)，\(k\) 为常数），因此 \(\displaystyle \lim_{x\rightarrow +\infty} \frac{\frac{x^{s-1}}{e^x}}{\frac{1}{x^2}} = \lim_{x\rightarrow +\infty} \frac{x^{s+1}}{e^x}\) ，从而根据比较判别法，对任意的 \(s\)，\(I_2\) 都收敛。

综上所述，当 \(s > 0\) 时，\(\Gamma(x)\) 收敛。

Gamma 函数的递推公式与解析延拓¶

由分部积分法，可以证明对所有的 \(s > 0\) 都有 \(\Gamma(s + 1) = s\Gamma(s)\)。

又 \(\displaystyle \Gamma(1) = \int_0^{+\infty} e^{-x} dx = 1\)，因此，\(\Gamma(n + 1) = n!\)（\(n \in \mathbb{Z}^+\)）

根据递推公式 \(\displaystyle \Gamma(s) = \frac{\Gamma(s + 1)}{s}\)，可以将区间 \((0, 1)\) 上的 Gamma 函数值延拓到区间 \((-1, 0)\) 上，同理，可以使得 Gamma 函数在所有除去非正整数上的点有定义。