语法分析：自底向上方法

语法分析器从词法分析器获得 Token 序列，确认该序列是否可以由语言的文法生成，然后： - 对于语法错误的程序，报告错误信息 - 对于语法正确的程序，生成语法分析树，例如抽象语法树（Abstract Syntax Tree, AST）

自底向上指的是，从输入的串出发，尝试将其归约到文法开始符号。以分析树（Parse Tree）的角度来看，自底向上方法从所有叶节点尝试构建出分析树。

Shift-Reduce¶

将输入的串使用分割符 | 分成两部分，在分割符 | 右侧的部分是仍未被分析器处理的终结符，而在分割符 | 左侧的部分既包含终结符又包含非终结符。

初始状态下，分割符 | 位于输入的串的第一个符号的左侧。在每一步，尝试对分割符 | 左侧的部分进行规约，如果不行，那么向右移动分割符 | 。

在串能够被接收的理想情况下，最终可以使用这种方法将串规约到 S |（其中 S 是文法的开始符号）并构建分析树。这是最右推导的逆过程。

下面图示这个方法¹：

LR 分析的一般模式是基于栈的 Shift-Reduce，其中，栈负责存储分割符 | 左侧的部分，分割符 | 右侧的部分则位于输入流中。在这个模式中，有四种行为，移动（Shift）、规约（Reduce）、错误（Error）和接受（Accept）。

LR(0) 语法分析¶

状态栈与 LR(0) 自动机¶

对于上面提到的，位于分割符 | 左侧的、被放置在栈中的串，通过维护一个状态（项/Item），记录它们凑出产生式的进度。

项（Item） 一个产生式加上在其右侧某处、代表进度的一个点 $\bullet$ 。例如产生式 $A \rightarrow \alpha \beta \gamma$ ，它可以拥有以下的项： $A \rightarrow \bullet \alpha \beta \gamma$ 、 $A \rightarrow \alpha \bullet \beta \gamma$ 、 $A \rightarrow \alpha \beta \bullet \gamma$ 、 $A \rightarrow \alpha \beta \gamma \bullet$ ，点 $\bullet$ 的左侧代表已经扫描到的部分，点 $\bullet$ 的右侧代表期望在接下来的输入中能够扫描到的部分（即：期望输入的字符串的头部能够由这部分推导得到）。

如果处于 $A \rightarrow \alpha \bullet \beta \gamma$ 状态的串读入了 $\beta$ ，那么它的状态会跳转为 $A \rightarrow \alpha \beta \bullet \gamma$ ，这个过程就类似于状态机，更贴切地，由于文法产生式是有限的、并且每个产生式右部的长度也是有限的，所以是有限状态机，这个有限状态机被称为 LR(0) 自动机，它用于帮助 LR 分析器判断当前栈顶内容是否可以进行规约。

为了方便表示起始状态与终结状态，添加一个新的开始符号 $S'$ 以及产生式 $S' \rightarrow S$ $（和对应的项），这里的$ 表示 EOF 的概念。

应用于 LR(0) 语法分析的 NFA¶

按以下方法，对每个项遍历，构造 NFA：

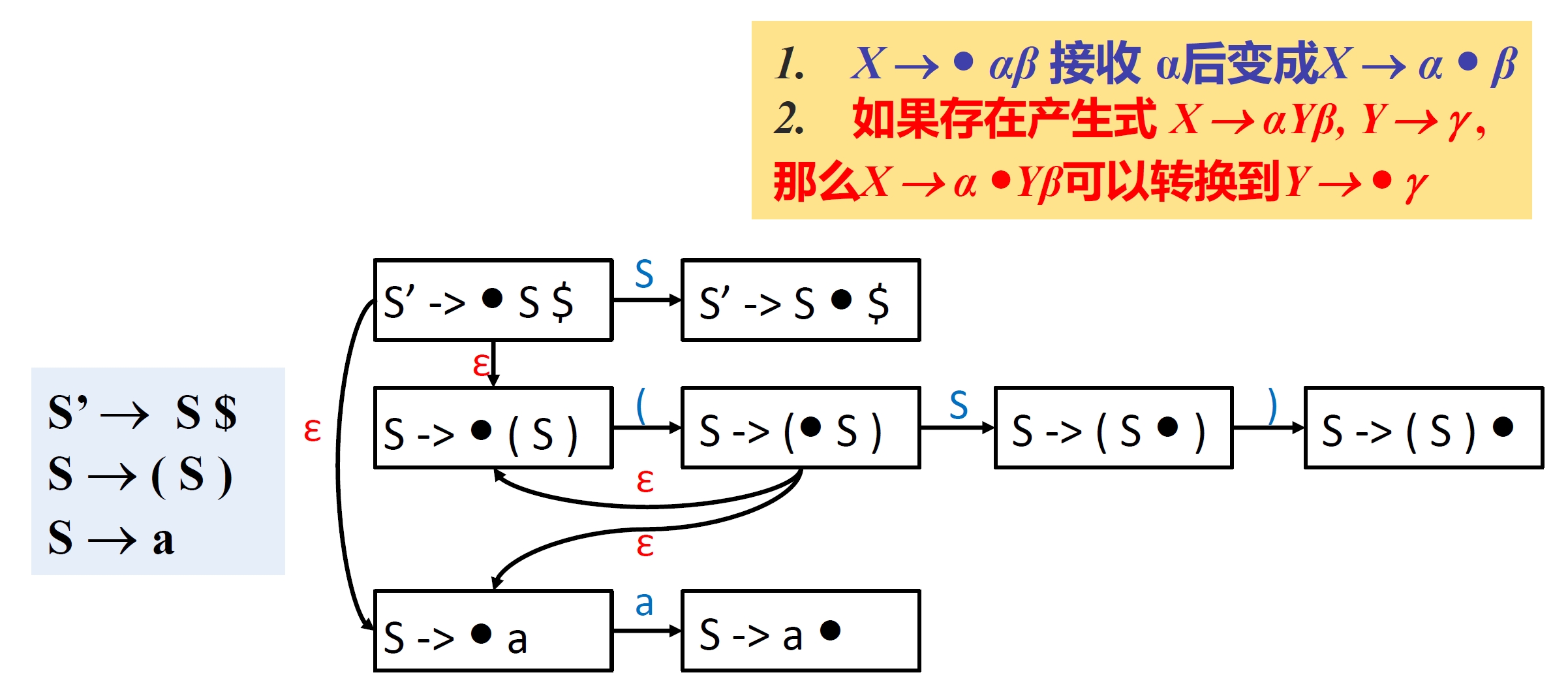
项 $X \rightarrow \bullet \alpha \beta$ 接收 $\alpha$ 后变成 $X \rightarrow \alpha \bullet \beta$ 。因此，添加从状态 $X \rightarrow \bullet \alpha \beta$ 到状态 $X \rightarrow \alpha \bullet \beta$ 的转移方式，条件是接收 $\alpha$ 。
如果存在产生式 $X \rightarrow \alpha Y \beta$ ， $Y \rightarrow \gamma$ ，则 $X \rightarrow \gamma \bullet Y \beta$ 可以无条件地（接收 $\varepsilon$ ）转移到 $Y \gamma \gamma$ 。（状态 $X \rightarrow \gamma \bullet Y \beta$ 表示希望看到由 $Y \beta$ 推导出的串，因此要先看到由 $Y$ 推导出的串，因此加上 $Y$ 的各个产生式对应的项）

一个简单的例子如图所示¹：

然后对于这个 NFA，用在正则语法的有限状态机中提到的方法，可以直接得到对应的 DFA。

应用于 LR(0) 语法分析的 DFA¶

我们可以跳过 NFA 而直接构造 DFA。这个方法被称为 Closure and GOTO Rules of LR(0) Automaton。

函数 $\text{Closure}(I)$ 和 $\text{GOTO}(I, X)$ 是两个子程序。

前者是期望规约过程下一个读到的非终结符（ $\bullet$ 符号右边第一个非终结符 $X$ ）作为产生式左部的所有产生式 $X \rightarrow \dots$ 。（这类似于正则语法 DFA 构造中的 $\varepsilon\text{-Closure}$ ，是因为如果期望看到由 $X\dots$ 推导出的串，必须先看到由非终结符 $X$ 推导出的串，所以需要看到 $X$ 的各个产生式，到 $X$ 的各个产生式的状态转移过程是无条件的）

后者是项 $I$ 接收输入 $X$ 后能够到达的项 $J$ 的 $\text{Closure}(J)$ 集合。

构造 DFA 的方法以以下伪代码给出：

Initialize T to {Closure({S' -> \bullet S\$})}
Initialize E to empty
repeat
    for each state I in T
        for each item "A -> \alpha \bullet X \beta" in I
            let J be Goto(I, X)
            T <- T \cup {J}
            E <- E \cup {I ->^X J}
until E and T did not change in this iteration

在一切的开始，只有一个状态，这个状态包含 $\text{Closure}(S' \rightarrow \bullet S \$)$ 的所有产生式。

对于每一个状态，检定其中每一个产生式，通过这个方法，我们得到 $\text{GOTO}()$ 函数的所有可能的第二个参数 $x$ ，令 $\text{GOTO}()$ 函数的第一个参数为当前检定的状态 $I$ ，求出 $\text{GOTO}(I, x)$ 以得到更多状态和状态之间的边。当状态和边都不再变化的时候，这个程序终止，我们得到所需要的 DFA。

图示这个过程¹：

语法分析表¶

根据 DFA，建立语法分析表。表中：s* 表示 shift into state ，r* 表示 reduce by rule ，accept 表示接收，g* 表示 goto state *。Action 表项的参数是状态 $I$ 和终结符 $a$ ，GOTO 表项的参数是状态 $I$ 和非终结符 $A$ 。

在这个网站，可以可视化地从任意的 LR(0) 文法构建对应的 DFA 以及语法分析表： https://lr0parser.com/

语法分析¶

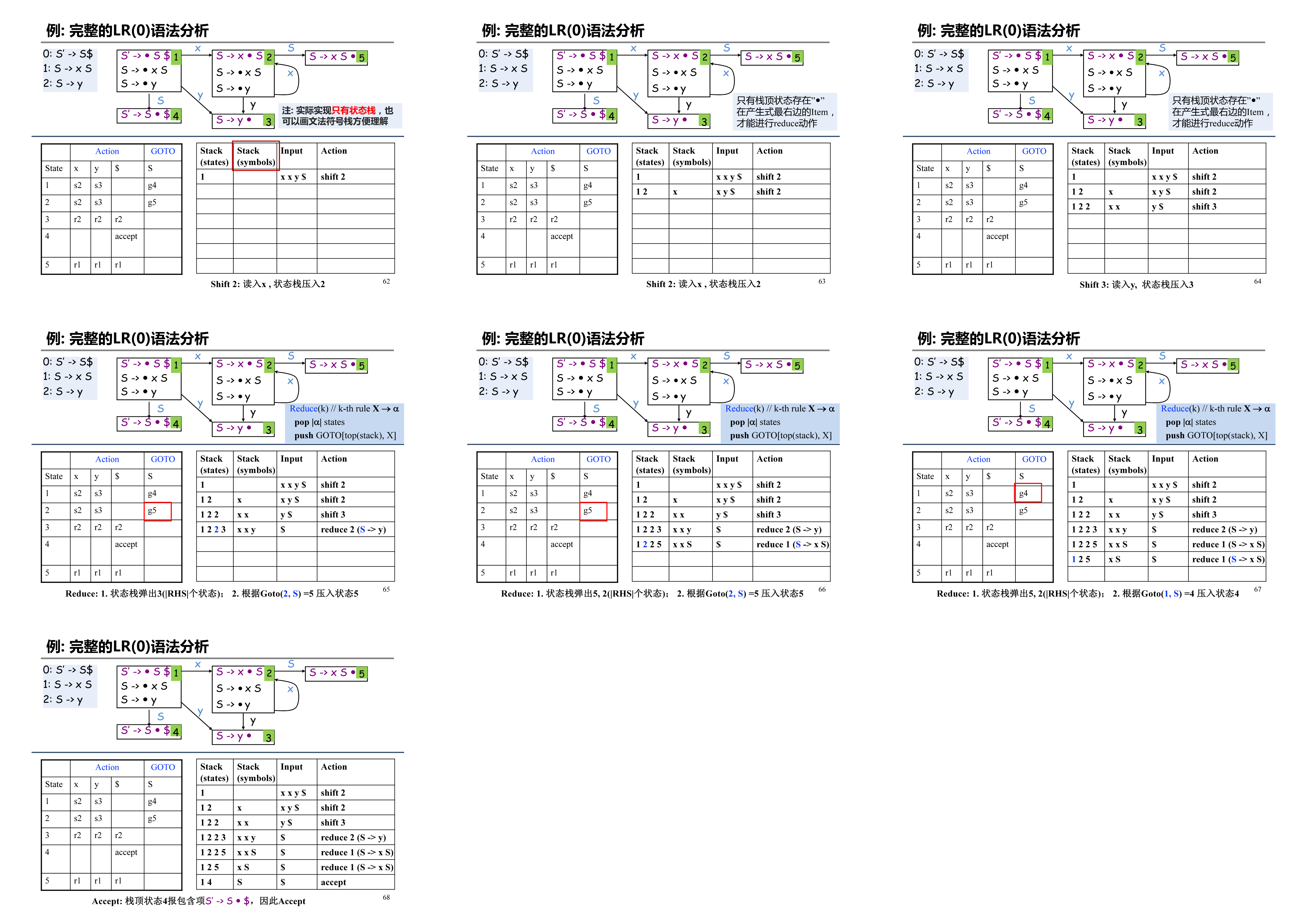
根据语法分析表，完成语法分析，这个过程遵循以下伪代码：

// 令 s 是栈顶状态, a 是 w$ 的第一个符号;
while (1) {
    // 一开始 s 为 Parsing DFA 的状态 1
    if (Action[s, a] == "shift s/") {
        将s/压入栈内;
        让a为下一个输入符号;
    } else if (Action[s, a] == "reduce A->b") {
        从栈顶弹出|b|个状态;
        令s/是当前栈顶状态,把GOTO[s/, A]入栈;
    } else if (Action[s, a] == "Accept") break;
    else error();
}

图示这个过程¹：

LR(0) 的局限性¶

可能会出现同一个状态同时有 shift 和 reduce 两个选择（S-R 冲突）或者多个 reduce 的目的状态（R-R 冲突），从而造成无法唯一确定动作。

SLR 语法分析¶

使用更加严格的归约条件以降低冲突的可能性。

由于规约条件更加严格，该语法的语法分析表有更小的可能冲突，因此可以识别更多文法。

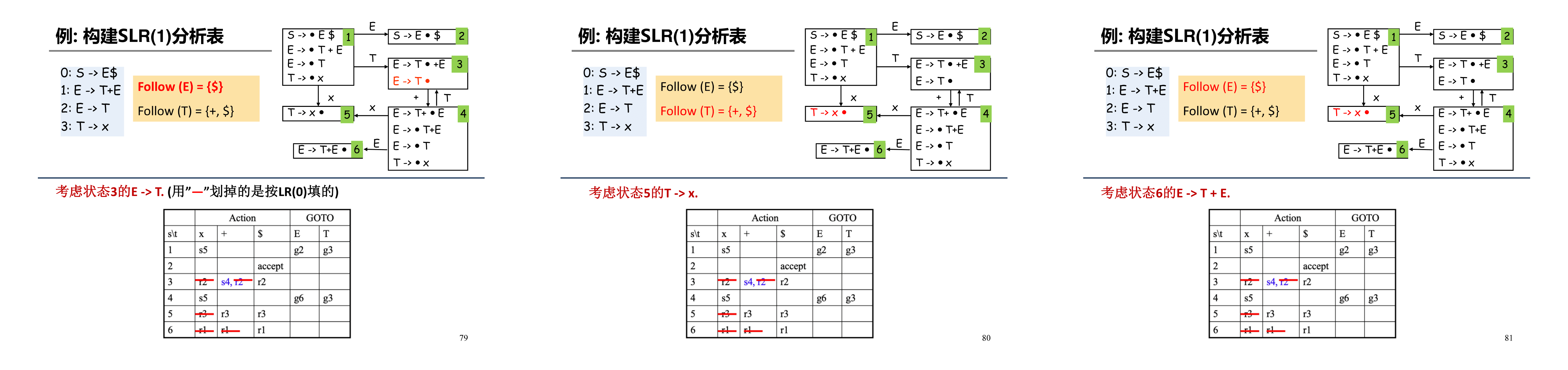
要求：被填入构造分析表的归约动作，只能是当输入的终结符属于产生式左部的 $\text{Follow}()$ 集合（即，能够以左部通过若干次推导得到的、紧邻左部的终结符）。

在 LR(0) 语法分析表的 Action 表项中，划去不符合条件的规约 $r\_$ （在 LR(0) 的语法分析表中， $r\_$ 将被填在一行中的每一个 Action 表项中），即可得到 SLR 语法分析表¹：

这个想法是类似 LL(1) 的：按照 $A \rightarrow \alpha$ 进行归约的条件是：下一个输入符号 $x$ 可以在某个句型中紧跟在 $A$ 之后，也就是 $x \in Follow(A)$ 。

然而，这仍然不能完全解决问题，因为如果 $\beta A x$ 不是任何最右句型的前缀，那么即使 $x$ 在某个句型中跟在 $A$ 之后，仍不应该按 $A \rightarrow \alpha$ 归约。

LR(1) 语法分析¶

通过添加lookahead 符号以指导归约，精确指明何时应该归约，是对 SLR 部分状态的分裂。

LR(1) 的项一般形如： $A \rightarrow \alpha \bullet \beta ,\ a$ ，这里的终结符 $a$ 就是 lookahead 符号。

这个项的含义是，存在于栈顶，已经扫描到的部分是 $\alpha$ ，期望输入的字符流的首部是能够由 $\beta a$ 推导得到的串，并且在读入 $\beta$ 推导得到的串后，根据产生式 $A \rightarrow \alpha \beta$ 规约时，期望输入的字符流的首部必须是终结符 $a$ 。

对于 LR(1) 的项 $A \rightarrow \alpha \beta \bullet,\ a$ 如果要进行规约，当且仅当字符流的下一个输入符号是 $a$ 。

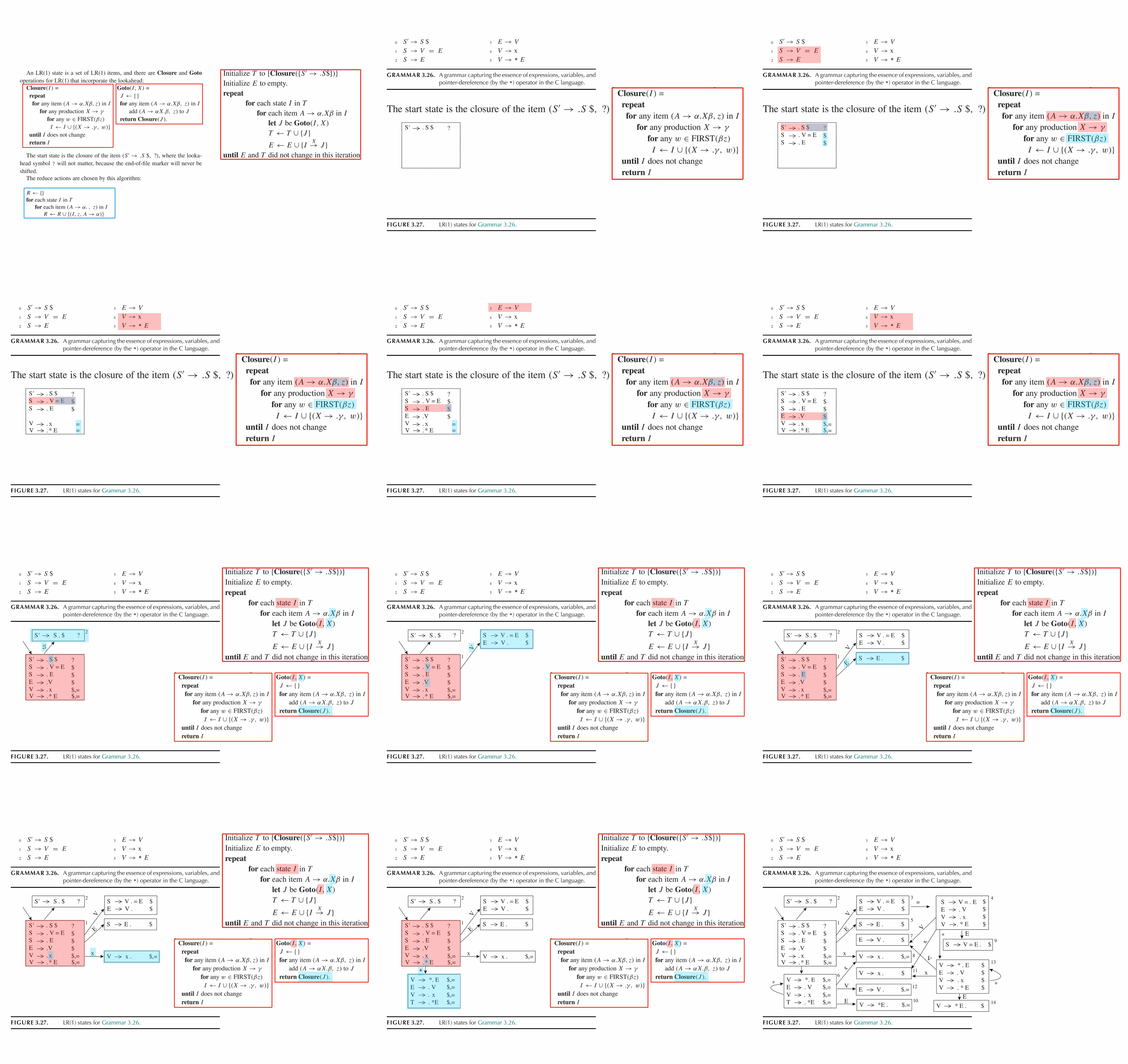
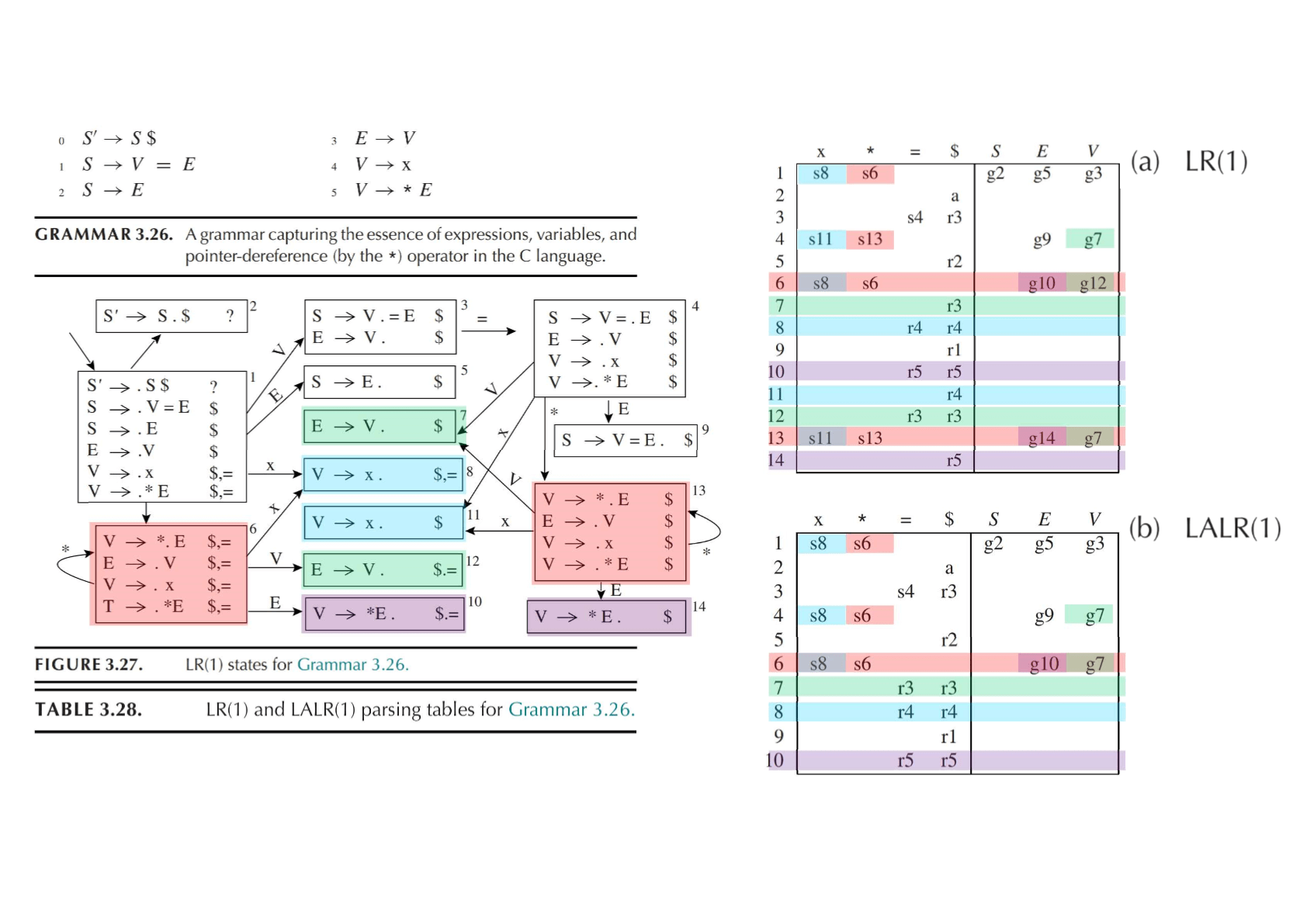
由于添加了 lookahead 符号，LR(1) 语法分析的 $\text{Closure}()$ 和 $\text{Goto}()$ 子程序相比 $LR(0)$ 的改变如下¹：

LR(1) 语法分析表的 Reduce Action 表项填写规则是：对于规约 $A \rightarrow \alpha \beta \bullet,\ a$ ，填写到坐标为 (当前状态, $a$ ) 的单元格中。其它表项填写规则以及 DFA 的生成与 LR(0)、SLR 一致。

LALR(1) 语法分析¶

对于 LR(1) 中的一些状态，它们包含相同的产生式与 $\bullet$ 符号位置，唯一的区别仅是 lookahead 符号不同。

LR(1) 状态 $\{(A \rightarrow \alpha \bullet \beta,\ a),(B \rightarrow \gamma \bullet \delta,\ b)\}$ 去掉所有的 lookahead 符号后，得到的集合 $\{(A \rightarrow \alpha \bullet \beta),(B \rightarrow \gamma \bullet \delta)\}$ 被称为状态的核心。

通过下面的方法，简化 LR(1) 的 DFA：

直到所有状态都有不同的核心，重复下面的过程：

选择两个具有相同核心的不同状态
合并被选择的状态，创建一个包含所有原来状态中的项的新状态
将所有指向原状态的边指向新状态；新状态指向所有原状态的后继状态

由于这实际上减弱了对规约的要求，所以 LALR(1) 只能够识别比 LR(1) 更少的文法。

错误恢复¶

Local Error Recovery¶

通过在文法中添加特殊的 $\text{error}$ 终结符以控制错误恢复的流程。

当 LR 语法分析器进入错误状态时，它会采取以下措施：

从状态栈中弹出元素（如有必要），直到达到对 error 的操作是移进的状态。
移进 error。
丢弃输入的符号（如有必要），直到达到在当前状态下具有非错误操作的 lookahead 符号。
恢复正常的语法分析过程。

下图展示了这个过程¹：

Global Error Recovery¶

不需要修改文法。

TODO。

LR(0), SLR, LR(1), LALR(1) 的关系¶

在规约条件上，LR(0) < SLR < LALR(1) < LR(1)，而规约条件越复杂的语法的语法分析表有越小的可能出现规约-规约或规约-移进冲突，因此可以识别越多的文法。从能够识别的文法的数量角度，同样有 LR(0) < SLR < LALR(1) < LR(1)。

在 SLR(1) 中，我们在决定一个状态是否应该进行规约操作时，只考虑了这个状态中所有项的后继符的集合（ $\text{Follow()}$ 集）。这种方法可能会导致一些不必要的冲突，因为并非所有的项都会在所有的后继符上进行规约。而在 LALR(1) 中，我们在决定一个状态是否应该进行规约操作时，会考虑每个项的 lookahead 集合。这是上面规约条件的连续不等式中 SLR < LALR(1) 的原因。

src:https://rainoftime.github.io/teaching/index.html ↩↩↩↩↩↩↩