语法分析：自顶向下方法

语法分析器从词法分析器获得 Token 序列，确认该序列是否可以由语言的文法生成，然后： - 对于语法错误的程序，报告错误信息 - 对于语法正确的程序，生成语法分析树，例如抽象语法树（Abstract Syntax Tree, AST）

自顶向下指的是，从文法的开始符号出发，尝试推导出输入的串。以分析树（Parse Tree）的角度来看，自顶向下方法从根节点出发，构建分析树。

描述编程语言的语法结构¶

为描述编程语言的语法结构，引入以下概念：

上下文无关文法（Context-Free Grammar, CFG）¶

上下文无关语言 \(L(G)\) 是正则语言 \(L(r)\) 的超集。

正则语言不能用于描述配对或嵌套的结构，原因在于有穷自动机无法记录访问同一状态的次数，因此不能够表达例如 \((^n)^n\) 的结构。正则语言是线性文法产生的所有句子的集合。

\[ G = (T, N, P, S) \]

\(T\) - 终结符集合（Terminals）：组成串的基本符号（token），例如 \(T = \{num, +, -\}\)

\(N\) - 非终结符集合（Non-terminals）：语法变量，最终应通过产生式与终结符组合成串，例如 \(N = \{expr, stmt\}\)

\(P\) - 产生式集合（Productions）：产生式描述将终结符和非终结符组合成串的方法，例如 \(E \rightarrow E + E\ |\ (E)\ |\ id\)

\(S\) - 开始符号（Start symbol）：某一个特定非终结符。它对应的串的集合就是文法的语言。

上下文无关文法的含义是，对于推导 \(\alpha A \beta \Rightarrow \alpha \gamma \beta\) 来说，符号串 \(\gamma\) 仅仅根据产生式 \(A \rightarrow \gamma\) 推导，而与 \(A\) 的上下文 \(\alpha\)，\(\beta\) 无关。

推导与规约¶

推导与规约是产生式和非终结符之间的转换过程，它们拥有相反的含义。以产生式 \(A \rightarrow \gamma\) 、串 \(\alpha A \beta\) 为例：

直接推导 把产生式看成重写规则，把符号串中的非终结符用其产生式右部的串来代替。

用符号 \(\Rightarrow\) 表示直接推导，\(\alpha A \beta \Rightarrow \alpha \gamma \beta\)

直接规约 把符号串中的某一部分用某一个产生式左部来代替。

即如果 \(\alpha A \beta \Rightarrow \alpha \gamma \beta\) ，则称 \(\alpha \gamma \beta\) 直接规约到 \(\alpha A \beta\)

最左推导 指的是每步总是代换最左边的非终结符。在自顶向下的语法分析中，总是采用最左推导的方式。

最左规约 是最右推导的反过程，在自底向上的语法分析中，总是采用最左归约的方式。

句型、句子、语言¶

句型（Sentential form） - 对开始符号为 \(S\) 的文法 \(G\) 如果从 \(S\) 出发能够经过零步或一步或若干步推导得到 \(\alpha\)，则称 \(\alpha\) 是 \(G\) 的一个句型。句型可以包含终结符、非终结符，也可以是空串。

句子（Sentence） - 句子是指不含非终结符的句型。

语言（Language） - 语言是指由文法 \(G\) 推导出的所有句子构成的集合，用 \(L(G)\) 表示。

编程语言文法¶

上下文无关文法也是编程语言文法的超集。因为上下文无关文法仍然可能具有二义性，而编程语言的文法通常是无二义的。

如果文法的某些句子存在不止一棵分析树，则称该文法是二义的，例如：

产生式 \(E \rightarrow E + E\ |\ E \times E\ |\ (E)\ |\ id\)

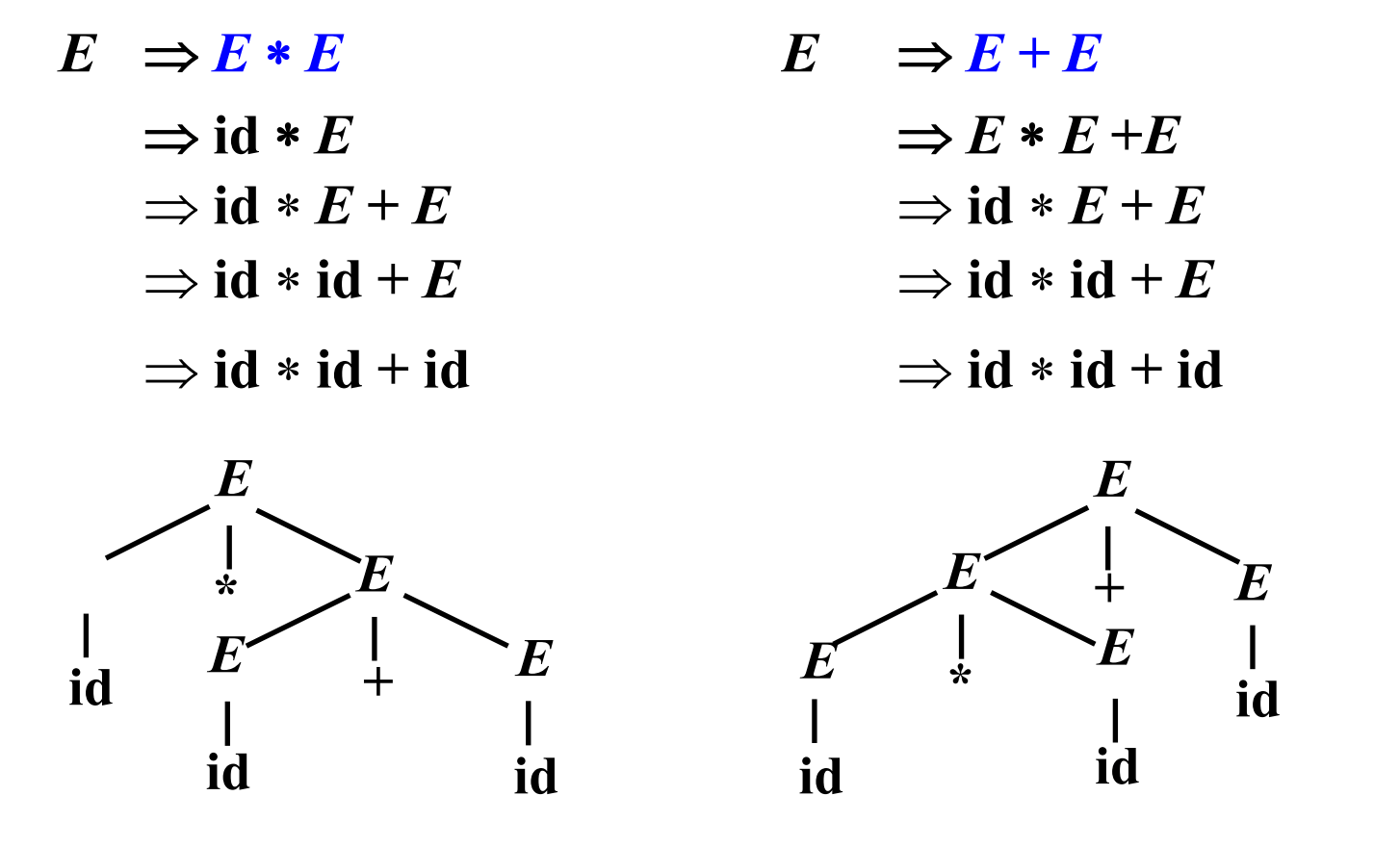
对于句子 \(id \times id + id\) 存在两棵不同的分析树¹：

在编程语言文法的情形下，如果令从左往右的三个 \(id\) 分别为 \(3,4,5\)，则这两棵分析树将分别导出 \(3\times(4 + 5)\) 和 \((3\times 4) + 5\)，这显然是不可以接受的。

将文法进行分层，规定在最左推导中更深层的非终结符总是会被优先替换，确保只有一种最左推导，可以消除上面的二义性问题。这是消除二义性的的惯用技术：分层，它需要规定符号的优先级以及规定符号的结合性。

我们首先考虑符号的优先级（终结符大于非终结符，括号大于乘法大于加法），将产生式改写为：

\[ \begin{array}{rl} E \rightarrow & E + E \\ | & E \times E \\ | & (E)\ |\ id \end{array} \]

然后考虑符号的结合性，将上面的产生式进一步改写为：

\[ \begin{array}{l} E \rightarrow E + T\ |\ T \\ T \rightarrow T \times F\ |\ F \\ F \rightarrow (E)\ |\ id \end{array} \]

这里的改写方法是：

（优先级）根据算符不同的优先级，为每一个算符引入新的非终结符，越接近开始符号的算符优先级越低
（结合性）递归非终结符在终结符左边，运算就左结合，反之就右结合，例如上面的 \(+\) 与 \(\times\)

递归下降分析（Recursive-Descent Parsing）¶

使用递归实现的穷举法，对于非终结符 \(A\) ，利用它的文法规则 \(A \rightarrow X_1\ |\ X_2\ |\ \dots\ |\ X_k\)，穷举所有选择。对于每一个选择 \(X_i\)，调用对应的处理过程： - 如果 \(X_i\) 是一个非终结符，递归调用非终结符 \(X_i\) 对应的处理过程 - 如果 \(X_i\) 是一个终结符 \(a\)，匹配输入串中对应的终结符 \(a\)

如果选择了不合适的产生式，得到一个非预期的串，则回溯。

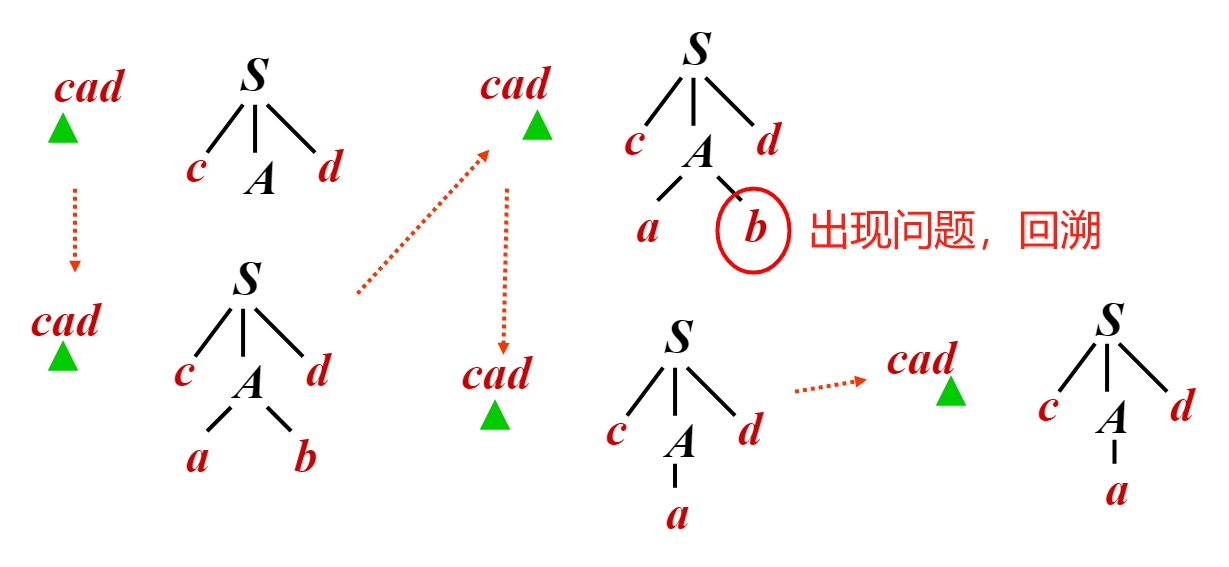
例如，文法 \(S \rightarrow cAd\)，\(A \rightarrow ab\ |\ a\)，考虑输入串 \(cad\) 的分析树¹：

由于往往需要对多个非终结符进行推导展开，因此尝试的路径可能呈指数级爆炸。

预测分析法（Predictive Parsing）¶

\(LL(k)\) 文法¶

L = left-to-right （从左到右扫描）

L = leftmost derivation （最左推导）

k = 向前看 \(k\) 个 Token 来确定产生式

\(LL(1)\) 文法¶

\(LL(1)\) 文法：每次为最左边的非终结符号选择产生式时，向前看 \(1\) 个输入符号，预测要使用的产生式。

\(\text{First}(\alpha) ::= \{a | \alpha \Rightarrow^* a\dots,a \in T\}\)，即：可从 \(\alpha\) 推导得到的串的首个终结符的集合。

\(\text{Follow}(A) ::= \{a | S \Rightarrow^* \dots Aa\dots, a \in T\}\)，即：从开始符号 \(S\) 出发，可能在推导过程中跟在 \(A\) 右边的终结符的集合。

\(\text{Nullable}(A) ::= \text{whether A can derive } \varepsilon\)，即：从非终结符 \(A\) 出发，是否能推导出空串。

为确保产生式选择的唯一性，\(LL(1)\) 文法中的任何产生式 \(A \rightarrow \alpha\ |\ \beta\)，其 \(\alpha\) 和 \(\beta\) 都需要满足（定义）：

\(\text{First}(\alpha) \cap \text{First}(\beta) = \varnothing\)（即：\(\alpha\) 与 \(\beta\) 不能推导出以同一个字符为首的串）
若 \(\beta \Rightarrow^* \varepsilon\)，那么 \(\alpha \nRightarrow^* \varepsilon\)，且 \(\text{First}(\alpha) \cap \text{Follow}(A) = \varnothing\)（即：\(\alpha\) 与 \(\beta\) 不能同时推导出 \(\varepsilon\)。在 \(\beta\) 能推导出空串的情形下，\(\alpha\) 可能推导出的串的首部不应该出现在可能在推导过程中跟在 \(A\) 右边的终结符号集中）

\(LL(1)\) 文法满足以下三个性质：

\(LL(1)\) 文法是无二义的
\(LL(1)\) 文法是无左递归的（即：不存在 \(A \rightarrow^* A\alpha\)）
\(LL(1)\) 文法是无左公因子的（即：不存在 \(X \rightarrow \alpha\beta\ |\ \alpha\gamma\)）

消除左递归¶

对于产生式 \(A \rightarrow^* A\alpha\ |\ \beta\)，其中 \(\alpha \neq \varepsilon\)，\(\beta \neq \varepsilon\)，\(A \notin \text{First}(\alpha)\)，\(A \notin \text{First}(\beta)\)：通过以下方法将这个文法限制为仅含右递归、不含左递归的形式：

\[ \begin{array}{l} A \rightarrow \beta A'\\ A' \rightarrow \alpha A'\ |\ \varepsilon \end{array} \]

观察：去掉 \(A\alpha \alpha \dots\) 的病态情形之后，由 \(A\) 生成的串只能以某个 \(\beta\) 开头，然后跟上零个或多个 \(\alpha\)。

消除左公因子¶

对于产生式 \(X \rightarrow \alpha\beta\ |\ \alpha\gamma\)，使用下面的产生式替换：

\[ \begin{array}{l} X \rightarrow \alpha X'\\ X' \rightarrow \beta\ |\ \gamma \end{array} \]

通过改写产生式来推迟决定，等读入了足够多的输入，获得足够信息后再做选择。

\(LL(1)\) 的预测分析法（递归下降实现）¶

计算所有非终结符的 \(\text{First}()\)，\(\text{Follow}()\)，\(\text{Nullable}()\)
构造预测分析表
根据预测分析表上的内容，即可通过向前看一个输入符号来唯一地确定选择哪个产生式

计算所有非终结符的 \(\text{Nullable}()\)，\(\text{First}()\)，\(\text{Follow}()\)¶

\(\text{Nullable}()\)¶

根据 \(\text{Nullable}()\) 的归纳定义 base case 以及 inductive case，迭代地从 base case 开始计算，直到所有非终结符的 \(\text{Nullable}()\) 不再变化。初始状态下，令所有非终结符的 \(\text{Nullable}()\) 为 False。

图示这个过程¹：

\(\text{First}()\)¶

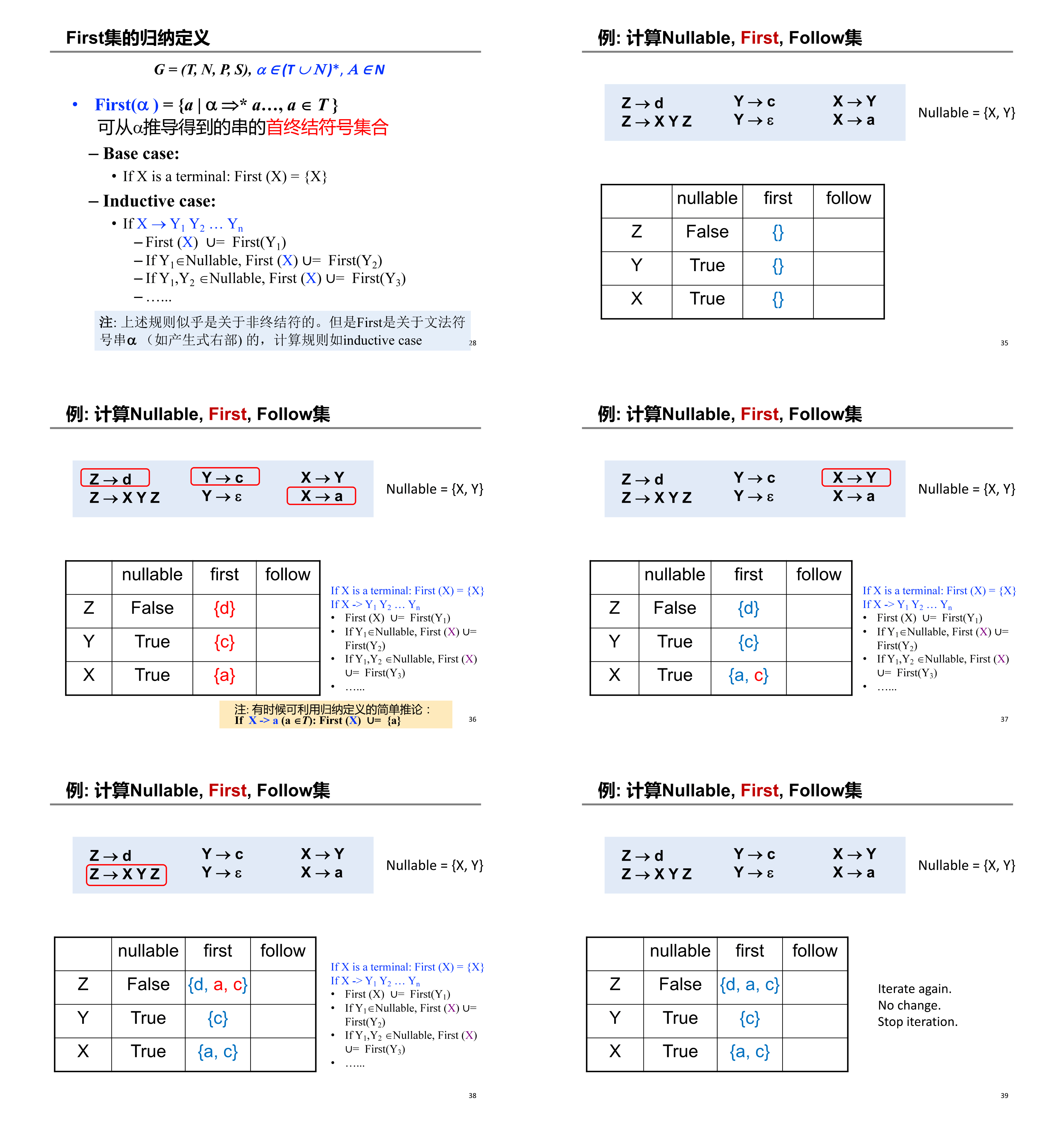
根据 \(\text{First}()\) 的归纳定义 base case 以及 inductive case，迭代地从 base case 开始计算 \(\text{First}()\) 不再变化。初始状态下，令所有非终结符的 \(\text{First}()\) 为 \(\varnothing\)。

图示这个过程¹：

\(\text{Follow}()\)¶

根据 \(\text{Follow}()\) 的归纳定义 base case 以及 inductive case，迭代地从 base case 开始计算 \(\text{Follow}()\) 不再变化。初始状态下，令所有非终结符的 \(\text{Follow}()\) 为 \(\varnothing\)。

图示这个过程¹：

构造预测分析表¶

以非终结符为行，终结符为列建表。预测分析表初始是空的。检定文法中的每一个产生式 \(A \rightarrow \alpha\)，按以下的规则填充分析表的 \(A\) 行某列单元格：

for each production "A -> \alpha"
    for each a \in first(\alpha)
        add "A -> \alpha" to T[A, a]
    if \varepsilon \in first(\alpha) then
        for each b \in follow(A)
            add "A -> \alpha" to T[n , b]

或者引入 \(\text{Nullable}\) 的概念时：

for each production "A -> \alpha"
    for each a \in first(\alpha)
        add "A -> \alpha" to T[A, a]
    if \alpha is Nullable then
        for each a \in follow(A)
            add "A -> \alpha" to T[A, a]

注意这里的 \(\alpha\) 可能是由若干终结符与非终结符组合而成的右部（例如 \(E \rightarrow A\ B\ \gamma\)），对于 \(\text{First}(A\ B\ \gamma)\) ，应当参照上面计算 \(\text{First}(A)\) 之相同方法。也可以利用已经生成好的所有非终结符的 \(\text{First}()\) 集合：

对于产生式 \(E \rightarrow E_1\ E_2\ E_3\ \dots \ E_n\)：

令右部 \(\text{First}(\text{RHS})\) 集初始为空。

顺序检定终结符或非终结符 \(E_i\)，从 \(i = 1\) 开始：

如果 \(E_i\) 是终结符 \(t\)：
- 如果 \(t \neq \varepsilon\)，则将 \(t\) 并入 \(\text{First}(\text{RHS})\) 集，然后终止检定
- 如果 \(t = \varepsilon\)，则将 \(\varepsilon\) 并入 \(\text{First}(\text{RHS})\) 集，然后检定 \(E_{i+1}\)
如果 \(E_i\) 是非终结符：
- 如果 \(\text{Nullable}(E_i) = 0\)，则将 \(\text{First}(E_i)\) 并入 \(\text{First}(\text{RHS})\) 集，然后终止检定
- 如果 \(\text{Nullable}(E_i) = 1\)，则将 \(\text{First}(E_i)\) 并入 \(\text{First}(\text{RHS})\) 集，然后检定 \(E_{i+1}\)

如图所示²（注意每一张子图中的算法最后一行有一点错误，应该为 add "A -> \alpha" to T[n , b]）：

可以证明，对于 \(LL(1)\) 文法，预测分析表的每一个单元格要么没有元素，要么只有一个元素。

\(LL(1)\) 语法分析器可视化： https://www.cs.princeton.edu/courses/archive/spring20/cos320/LL1/

错误恢复¶

如果语法分析器的接收的 token 流不是文法所能够接受的，语法分析器需要抛出异常并停止语法分析，然后打印错误信息并从错误中恢复。

我们可以通过删除、替换、插入 token 来从错误中恢复。其中，插入 token 是存在风险的，因为这可能使得语法分析器不会停止；而删除 token 则不会遇到无限循环的问题，这是因为我们总会碰到 token 流的 EOF 然后停止我们的语法分析器。

一个通过删除 token 实现的从错误中恢复的方法是，按顺序跳过 token 流中所有不在当前分析的非终结符之 \(\text{Follow}()\) 集合中的 token。