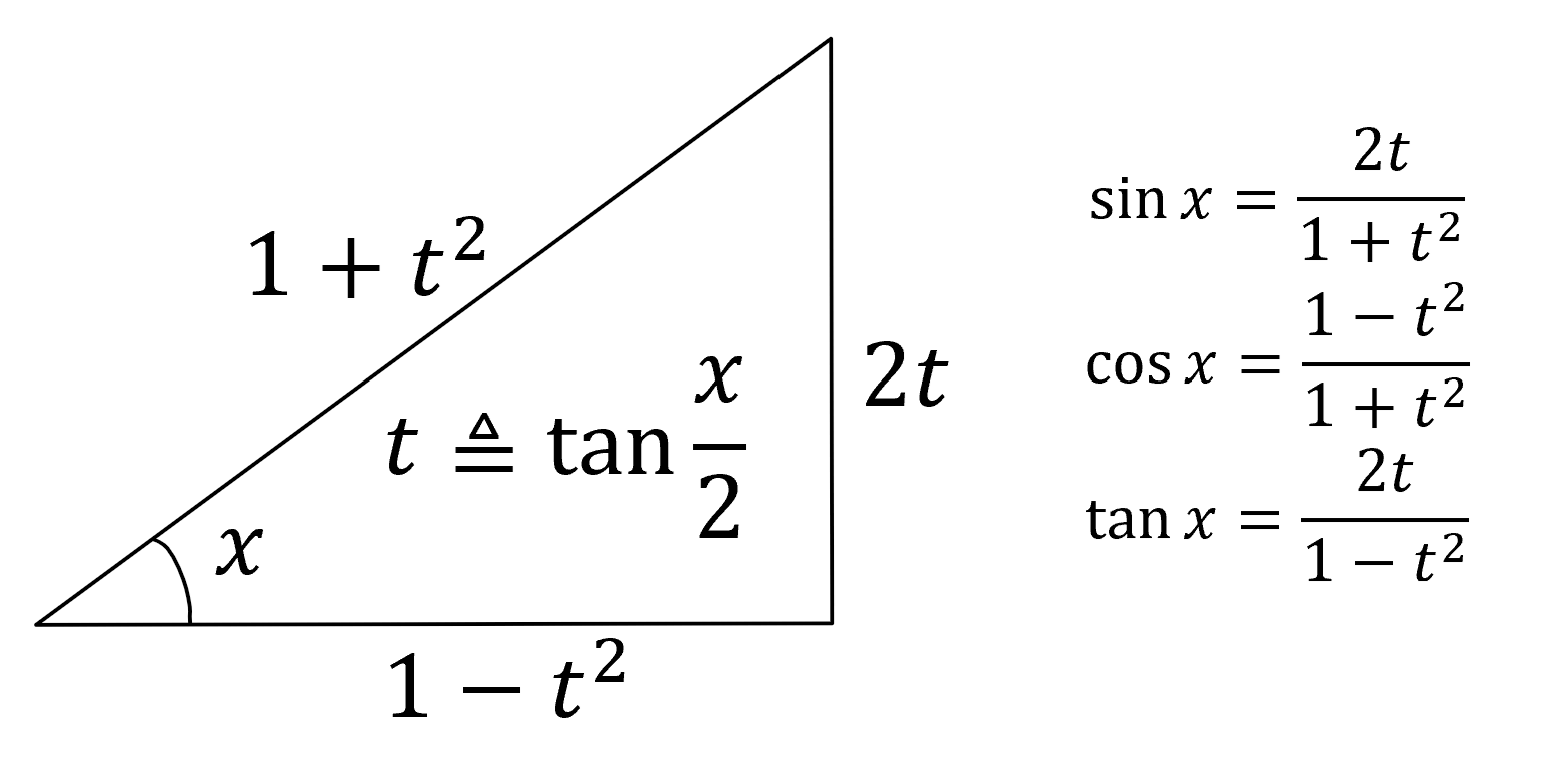一元函数的不定积分

本文详细介绍了一元函数的不定积分及其应用。首先定义了不定积分的概念，解释了反导数和原函数的关系。接着，讨论了原函数的存在性条件，并介绍了不定积分的基本运算法则，包括凑微分法、换元法和分部积分法。随后，文章探讨了常见类型的不定积分的计算方法，如有理函数、三角有理式和分段函数的不定积分。通过本文，读者可以全面掌握一元函数不定积分的基本理论和计算技巧。

（摘要由 OpenAI GPT 4o 生成）

定义 对于函数 $f(x)$，如果存在某个可微函数 $F(x)$ 对定义区间 $I$ 上的所有 $x$，都有 $F'(x) = f(x)$，则称 $F(x)$ 为函数 $f(x)$ 的反导数或一个原函数。函数 $f(x)$ 的所有反导数（或称原函数，下文中统一称为原函数）称为函数 $f(x)$ 的不定积分，用记号 $\displaystyle \int f(x) dx$ 表示，$\displaystyle \int$ 是积分号，$x$ 是积分变量，$f$ 是被积函数。

可以粗略地认为，对变量 $x$ 的不定积分运算 $\displaystyle \int \dots dx$ 是求导运算 $\displaystyle \frac{d}{dx}$ 的逆运算。

原函数的存在性

若函数 $f(x)$ 在区间 $I$ 上连续， 则 $f(x)$ 在区间 $I$ 上必有原函数。

若函数 $f(x)$ 在区间 $I$ 上有第一类间断点或无穷间断点， 则 $f(x)$ 在区间 $I$ 上必没有原函数。

Note

函数间断点要求 $f(x_0)$ 存在，而 $f(x_0^+)$ 与 $f(x_0^-)$ 和 $f(x_0)$ 不相等（或前两者不存在）。如果是 $f(x_0)$ 本身无定义，那么这个点不是间断点。如果 $f(x_0)$ 本身无定义，但是 $f(x_0^+) = f(x_0^-)$，那么函数在包含这个点的区间上是可以有原函数的。

反之，若 $F(x)$ 可导，导函数不连续的唯一可能是 $F'(x)$ 在某点为震荡间断点。

Note

对 $\displaystyle F(x) = \int_0^x f(t) dt$，如果这里的 $f(x)$ 不存在原函数，那么 $F(x)$ 可能在某点不可导。

原函数与不定积分

由定义我们可以知道，如果 $F(x)$ 是 $f(x)$ 的一个原函数，那么显然 $F(x) + C$ 也是 $f(x)$ 的原函数。并且，我们可以断言：除了这些函数以外，$f(x)$ 不会存在其他的原函数，下面将给出简要的证明。

证明. 我们首先证明两个引理：

[中值定理系1] 假设函数 $f(x)$ 在 $(a, b)$ 可导（$a,\ b$ 可取 $\pm \infty$），若 $\forall x \in (a, b)$，都有 $f'(x) = 0$，则对 $\forall x \in (a, b)$，都有 $f(x) = C$，其中 $C$ 是常数。

证明. 任取 $x_1 < x_2 \in (a, b)$，必然有 $f(x)$ 在 $[x_1, x_2]$ 连续、在 $(x_1, x_2)$ 可导。

对 $f(x)$ 在区间 $(x_1, x_2)$ 上使用拉格朗日中值定理，有 $\displaystyle \frac{f(x_1) - f(x_2)}{x_1 - x_2} = f'(\xi) = 0$，其中 $\xi$ 是介于 $x_1$ 与 $x_2$ 的一点。

因此，对于 $\forall x_1, x_2 \in (a, b)$，我们都能够证明 $f(x_1) = f(x_2)$，从而证明了 $f(x)$ 在区间 $(a, b)$ 上是一个常函数。$\blacksquare$

[中值定理系2] 假设函数 $f(x),\ g(x)$ 在 $(a, b)$ 可导（$a,\ b$ 可取 $\pm \infty$），并且 $\forall x \in (a,b)$ 都有 $f'(x) = g'(x)$，则存在某个常数 $C$，使得 $f(x) = g(x) + C$。

证明. 由导数的运算法则，可知 $[f(x) - g(x)]' = f'(x) - g'(x) = 0$。

由[中值定理系1]的结论，可知存在某个常数 $C$ 使得 $f'(x) - g'(x) = C$，即 $g'(x) = f'(x) + C$。$\blacksquare$

现在我们考虑原问题，假设 $G(x)$ 也是 $f(x)$ 的一个原函数，那么必然有 $G'(x) = f(x)$。

由于 $F(x)$ 是 $f(x)$ 的一个原函数，因此 $G'(x) = f(x) = F'(x)$。

根据[中值定理系2]，可知存在某个常数 $C_1$ 使得 $G(x) = F(x) + C_1$，这也就是说除了 $F(x) + C$以外，$f(x)$ 不会存在其他的原函数。$\blacksquare$

不定积分结果（在形式上）不唯一，求导即可验证积分结果的正确性。然而不同形式的不定积分结果之间，一定只相差一个任意常数。

有很大一部分的不定积分并不能通过使用常规的方法求解原函数，但这并不意味着这些函数不存在原函数（由于这些函数都符合不定积分存在性的要求，不能够说这些不定积分“不可积”），只是它们的原函数并不是初等函数。几个常见的不存在初等函数解的不定积分如下：

$$\begin{array}{c} \displaystyle \int e^{x^2} dx & \displaystyle \int \frac{e^x}{x} dx & \displaystyle \int \frac{1}{\ln x} dx & \displaystyle \int \frac{\sin x}{x} dx & \displaystyle \int \frac{\cos x}{x} dx & \dots \end{array}$$

不定积分的运算法则

由定义出发得到的运算法则

$$\begin{array}{cc} \displaystyle F'(x) = f(x) & \displaystyle \int f(x) dx = F(x) + C \\ \displaystyle (\int f(x) dx)' = f(x) & \displaystyle d\int f(x) dx = f(x) dx \\ \displaystyle \int f'(x) dx = f(x) + C & \displaystyle \int df(x) = f(x) + C \\ \end{array}$$

这些运算法则都可以通过不定积分的定义证明。

由求导规则得到的运算法则

$$\begin{array}{c} \displaystyle \int kf(x) dx = k \int f(x) dx \\ \displaystyle \int [f(x) \pm g(x)] dx = \int f(x) dx \pm \int g(x) dx \\ \boxed{\displaystyle \int udv = uv - \int vdu} \end{array}$$

以上的三条运算法则都可以通过求导运算法则得到证明。我们将简要证明第三条运算法则 $\displaystyle \int udv = uv - \int vdu$，这就是著名的分部积分法（integration by parts）。

证明1. 如果 $f$ 和 $g$ 是 $x$ 的可微函数，由导数的乘法法则可得：

$$\frac{d}{dx}[f(x) g(x)] = f'(x)g(x) + f(x)g'(x)$$

用以 $x$ 为积分变量的不定积分表示，则有：

$$\int \frac{d}{dx}[f(x) g(x)] dx = \int [f'(x)g(x) + f(x)g'(x)]dx$$

对等号两侧分别使用不定积分的运算性质，可得：

$$f(x)g(x) = \int f'(x)g(x) dx + \int f(x)g'(x) dx$$

对等号右侧使用微分的运算性质，可得：

$$f(x)g(x) = \int g(x) df(x) + \int f(x) dg(x)$$

如果令 $u = f(x)\ ,v = g(x)$，整理上式，即得 $\displaystyle \int udv = uv - \int vdu$。$\blacksquare$

证明2. 根据微分的乘法法则：

$$duv = udv + vdu$$

两边积分：

$$\int duv = \int (udv + vdu)$$

根据不定积分的运算性质，可得：

$$\int duv = \int udv + \int vdu$$

移项即可得到 $\displaystyle \int udv = uv - \int vdu$。$\blacksquare$

不定积分的计算

凑微分（第一类换元法）

如果 $\displaystyle \int f(x) dx = F(x) + C$，则利用微分运算的性质，我们可以计算下面的积分：

$$\int f(\varphi(x)) \varphi'(x) dx = \int f(\varphi(x)) d\varphi(x) = F(\varphi(x)) + C$$

此方法关键在于如何将被积函数分解为 $f(\varphi(x)) \varphi'(x)$ 的形式，或者换一个更加具体的说法：寻找原不定积分的某一种等价形式 $\displaystyle \int f_1(\varphi(x))f_2(x) dx$ ，将其中的 $f_2(x)d(x)$ 设法表示为 $d\varphi(x)$，这样我们只需要可以计算 $\displaystyle \int f_1(x) dx$ 就能计算原不定积分。

凑微分法需要我们熟记常见函数的导函数，以及时刻留意：

1. 为被求导函数添加常数项将不会影响求导结果。
   • $dx = d(x + C)$
   • $f'(x)dx = d(f(x) + C)$
2. 求导结果相差常数倍是可以接受的。
   • $\frac{dx}{\sqrt{x}} = 2d\sqrt{x}$
   • $dx = \frac{1}{a}d(ax + b)$
   • $xdx = -\frac{1}{2}d(a^2 - x^2)$
   • $xdx = \frac{1}{2}d(x^2 \pm a^2)$
3. 使用各种恒等变换（三角恒等变换等）变形被积函数，使其形式有利于凑微分。

例1. 求 $\displaystyle \int \tan x dx$

$$\begin{array}{ll} \displaystyle \int \tan x dx &= \displaystyle \int \frac{\sin x}{\cos x}dx \\ &= \displaystyle \int \frac{-d\cos x}{\cos x} \\ &= \displaystyle -\ln |\cos x| + C \end{array}$$

例2. 求 $\displaystyle \int \csc x dx = \int \frac{1}{\sin x} dx$

$$\begin{array}{ll} \displaystyle \int \frac{1}{\sin x} dx &= \displaystyle \int \frac{1}{2\sin \frac{x}{2} \cos \frac{x}{2}}dx \\ &= \displaystyle \int \frac{1}{\frac{\sin \frac{x}{2}}{\cos \frac{x}{2}} \cos^2 \frac{x}{2}}d\frac{x}{2} \\ &= \displaystyle \int \frac{1}{\tan \frac{x}{2}}d\tan \frac{x}{2} \\ &= \displaystyle \ln |\tan \frac{x}{2}| + C \\ &= \displaystyle \ln |\frac{1- \cos x}{\sin x}| + C \\ &= \displaystyle \ln |\csc x - \cot x| + C \end{array}$$

对特别复杂的式子，我们可以考虑优先处理式中最复杂的部分，例如分母中的某一个因子，尝试对其求导，然后在被积分式中的其他部分凑出这个导函数。

例3. 求 $\displaystyle \int \frac{\sin x \cos x}{\sqrt{a^2 \sin^2 x + b^2 \cos^2 x}} dx$，其中 $|a| \neq |b|$

$$\begin{array}{ll} \displaystyle \int \frac{\sin x \cos x}{\sqrt{a^2 \sin^2 x + b^2 \cos^2 x}} dx &= \displaystyle \int \frac{1}{2a^2 - 2b^2}\frac{2a^2 \sin x \cos x - 2b^2 \sin x \cos x}{\sqrt{a^2 \sin^2 x + b^2 \cos^2 x}} dx \\ &= \displaystyle \frac{1}{2a^2 - 2b^2} \int \frac{d(a^2 \sin^2 x + b^2 \cos^2 x)}{\sqrt{a^2 \sin^2 x + b^2 \cos^2 x}} \\ &= \displaystyle \frac{1}{2a^2 - 2b^2} \int (a^2 \sin^2 x + b^2 \cos^2 x)^{-\frac{1}{2}} d(a^2 \sin^2 x + b^2 \cos^2 x) \\ &= \displaystyle \frac {\sqrt{a^2 \sin^2 x + b^2 \cos^2 x}}{a^2 - b^2} + C \end{array}$$

此外，对于 $\displaystyle \frac{P(x)}{Q_1(x)Q_2(x)}$ 形式的被积函数，可以尝试在分子中通过加项减项的手段，结合不定积分的运算法则将积分式分解为形式更为简单的两个不定积分求和，这两个不定积分的分子分母在约分前应分别具有 $Q_1(x)$ 与 $Q_2(x)$ 的公因子。

例4. 求 $\displaystyle \int \frac{1}{a^2 - x^2} dx$

$$\begin{array}{ll} \displaystyle \int \frac{1}{a^2 - x^2} dx &= \displaystyle \int \frac{1}{(a + x)(a - x)} dx \\ &= \displaystyle \frac{1}{2a} \int \frac{(a + x) + (a - x)}{(a + x)(a - x)} dx \\ &= \displaystyle \frac{1}{2a}(\int \frac{a + x}{(a + x)(a - x)} dx + \int \frac{a - x}{(a + x)(a - x)} dx) \\ &= \displaystyle \frac{1}{2a}(\int \frac{-1}{a - x}d(a - x) + \frac{1}{a + x}d(a + x)) \\ &= \displaystyle \frac{1}{2a}(- \ln |a - x| + \ln |a + x| ) + C \\ &= \displaystyle \frac{1}{2a} \ln |\frac{a + x}{a - x}| + C \end{array}$$

之所以凑微分法又称为第一类换元法，是因为我们可以令微分算子中的表达式 $\varphi(x) = u$，这样原积分就变为 $\displaystyle \int f(u) du = F(u) + C$，最后再向积分结果中回代 $u = \varphi(x)$ 即可。

换元法（第二类换元法）

假设 $x = \varphi(t)$ 严格单调、可微，并且 $f(\varphi(t))\varphi'(t)$ 有原函数 $F(t)$，那么我们可以计算 $\displaystyle \int f(x) dx$：

$$\displaystyle \int f(x) dx = \int f(\varphi(t)) d\varphi(t) = \int f(\varphi(t))\varphi'(t) dt = F(t) + C = F(\varphi^{-1}(x)) + C$$

虽然从表达式上来看，似乎这复杂化了原积分，不过在实际运用中，我们通常会选取有利的 $x = \varphi(t)$ 使换元后的积分易于计算，从而达到简化积分的目的。

三角换元法对被积函数中存在以下形式的无理函数的情形是一个可选的方案：

$$\begin{array}{rcll} \displaystyle \sqrt{a^2 - x^2} & let & \displaystyle x = a\sin t,\ t \in [-\frac{\pi}{2}, \frac{\pi}{2}] & \displaystyle \sqrt{a^2 - x^2} = |a \cos t| \\ \displaystyle \sqrt{a^2 + x^2} & let & \displaystyle x = a\tan t,\ t \in (-\frac{\pi}{2}, \frac{\pi}{2}) & \displaystyle \sqrt{a^2 + x^2} = |a \sec t| \\ \displaystyle \sqrt{x^2 - a^2} & let & \displaystyle x = a\sec t,\ t \in [0, \frac{\pi}{2}) \cup (\frac{\pi}{2}, \pi] & \displaystyle \sqrt{x^2 - a^2} = |a \tan t| \end{array}$$

上面的换元方案主要的思想是利用三角恒等式，从而达到去除根式的目的。

在选用三角换元法时，可以画出对应的直角三角形（其中一锐角为 $t$），求出直角三角形的各边长，然后根据三角函数的定义，方便地求出 $t$ 的各个三角函数，从而将换元后求得的原函数中的 $t$ 替换回 $x$。

除此之外，面对根式还有一些换元方案，它们的主要思路是只要从换元式 $\psi(t) = \phi(x)$ 可以轻松地求得 $x = \varphi(t)$（主要是使得经过变换过的 $\psi(t) = \phi(x)$ 中的 $x$ 仅存在一次项），就能够运用第二类换元法尝试达到化简（有理化）被积分函数得目的。这是符合寻常的换元法由繁至简的思想的。

$$\begin{array}{c} \displaystyle \sqrt[n]{\frac{ax + b}{cx + d}} & let & \displaystyle \sqrt[n]{\frac{ax + b}{cx + d}} = t & i.e. & \displaystyle x = \frac{dt^n - b}{a - ct^n} \end{array}$$

著名的欧拉代换：

$$\begin{array}{rcccc} \displaystyle \sqrt{ax^2 + bx + c}\ (a > 0) & let & \displaystyle \sqrt{ax^2 + bx + c} = t \pm \sqrt{a}x & i.e. & \displaystyle x = \frac{t^2 - c}{x \mp 2\sqrt{a}t} \\ \displaystyle \sqrt{ax^2 + bx + c}\ (c > 0) & let & \displaystyle \sqrt{ax^2 + bx + c} = xt + \sqrt{c} & i.e. & \displaystyle x = \frac{2\sqrt{c}t - b}{a - t^2} \\ \displaystyle \sqrt{ax^2 + bx + c} = \sqrt{a(x - \alpha)(x - \beta)} & let & \displaystyle \sqrt{a(x - \alpha)(x - \beta)} = t(x - \alpha) & i.e. & \displaystyle x = \frac{\alpha t^2 - a\beta}{t^2 - a} \end{array}$$

Note

$a < 0$ 并且 $c < 0$ 并且方程 $ax^2 + bx + c = 0$ 实数根的这种情况，无理函数 $\sqrt{ax^2 + bx + c}$ 在整个实数域上没有定义。

第二类换元法并不局限于以上几种类型，只要通过适当的变量代换能将复杂的不定积分转化为较容易的不定积分，都可以采用第二类换元法。

分部积分法

利用 $\displaystyle \int u dv = uv - \int v du$ 简化原不定积分 $\displaystyle \int u dv$ 的计算，其基本原则是 $\displaystyle \int v du$ 比 $\displaystyle \int u dv$ 更容易计算。

坊间流传这样的口诀：“反对幂指三”，在英语使用者中，与之对应的口诀为 LIATE rule，其含义是出现在口诀中较左侧的函数应该出现在被积函数的式中，而出现在较右侧的函数应该出现在微分式中（即，$u$ 的选取顺序为：反三角函数 & 对数函数 > 幂函数 > 指数函数 & 三角函数）。

对于多数能够直接使用分部积分法一步到位的题目，只需要都试一下就行了。对于需要多次分部积分的题目，也可以简单地对分部积分后产生的新不定积分的计算复杂程度与原积分式进行比较，以决定是否应该换一种分部积分的方式。

分部积分法有以下三种常见的应用情形：

第一种应用情形为上面已经讨论过的， $\displaystyle \int v du$ 比 $\displaystyle \int u dv$ 更容易计算；或是 $du = u'dx$ 中 $u'$ 的形式与 $v$ 的形式相似（常常是在 $u$ 为反三角函数的情况中），以达到化简不定积分计算的目的。

例5. 求 $\displaystyle I = \int \ln x dx$

$$\begin{array}{ll} \displaystyle \int \ln x dx &= \displaystyle x \ln x - \int x d\ln x \\ &= \displaystyle x \ln x - \int 1 dx \\ &= \displaystyle x \ln x - x + C \end{array}$$

例6. 求 $\displaystyle I = \int \frac{xe^x}{\sqrt{e^x - 1}}dx$

$$\begin{array}{ll} \displaystyle \int \frac{xe^x}{\sqrt{e^x - 1}}dx &= \displaystyle 2 \int x d\sqrt{e^x - 1} \\ &= \displaystyle 2x\sqrt{e^x - 1} - 2\boxed{\int \sqrt{e^x - 1} dx} \\ \end{array}$$

令 $\sqrt{e^x - 1} = t$，则 $x = \ln (t^2 + 1)$，计算框起部分的积分：

$$\begin{array}{ll} \displaystyle \boxed{\int \sqrt{e^x - 1} dx} &= \displaystyle \int t d\ln (t^2 + 1) \\ &= \displaystyle \int \frac{2t^2}{t^2 + 1} dt \\ &= \displaystyle 2 \int \frac{1}{1 + (\frac{1}{t})^2} dt \\ &= \displaystyle 2 \arctan \frac{1}{t} + C \\ &= \displaystyle 2 \arctan \frac{1}{\sqrt{e^x - 1}} + C \end{array}$$

则有：

$$\int \frac{xe^x}{\sqrt{e^x - 1}}dx = \displaystyle 2x\sqrt{e^x - 1} - 4 \arctan \frac{1}{\sqrt{e^x - 1}} + C$$

例7. 求 $\displaystyle I = \int x \arctan x dx$

$$\begin{array}{ll} \displaystyle \int x \arctan x dx &= \displaystyle \frac{1}{2} \int \arctan x dx^2 \\ &= \displaystyle \frac{1}{2} x^2\arctan x - \frac{1}{2}\int x^2 d\arctan x \\ &= \displaystyle \frac{1}{2} x^2\arctan x - \frac{1}{2}\int \frac{x^2}{1 + x^2} dx \\ &= \displaystyle \frac{1}{2} x^2\arctan x - \frac{1}{2}\arctan \frac{1}{x} + C \end{array}$$

第二种应用情形为不定积分经过若干次分部积分后，会再次产生原先的不定积分。这是由于有一些函数求导后的形式不会发生变化，例如一次情形的 $e^x$，两次情形的 $\sin x$ 与 $\cos x$。这样，我们通过解线性方程（组）就能够求得原不定积分的值。

例8. 求 $\displaystyle I_1 = \int e^{ax}\cos(bx) dx$ 与 $\displaystyle I_2 = \int e^{ax}\sin(bx) dx$

$$\begin{array}{ll} \displaystyle \boxed{I_1} = \int e^{ax}\cos(bx) dx &= \displaystyle \frac{1}{a} \int \cos(bx) de^{ax} \\ &= \displaystyle \frac{1}{a} [\cos(bx) e^{ax} - \int e^{ax} (-b\sin(bx))dx] \\ &= \displaystyle \frac{1}{a} \cos(bx) e^{ax} + \frac{b}{a} \int e^{ax} \sin(bx)dx \\ & \boxed{= \displaystyle \frac{1}{a} \cos(bx) e^{ax} + \frac{b}{a} I_2} \\ \displaystyle \boxed{I_2} = \int e^{ax}\sin(bx) dx &= \displaystyle \frac{1}{a} \int \sin(bx) de^{ax} \\ &= \displaystyle \frac{1}{a} [\sin(bx) e^{ax} - \int e^{ax} (b\cos(bx))dx] \\ &= \displaystyle \frac{1}{a} \sin(bx) e^{ax} - \frac{b}{a} \int e^{ax} \cos(bx)dx \\ & \boxed{= \displaystyle \frac{1}{a} \sin(bx) e^{ax} - \frac{b}{a} I_1} \end{array}$$

求解框起的有关 $I_1$，$I_2$ 的线性方程组，即可得到：

$$\left\{ \begin{array}{l} \displaystyle I_1 = \int e^{ax}\cos(bx) dx = \frac{e^{ax}}{a^2 + b^2}(b\sin(bx) + a\cos(bx)) + C \\ \displaystyle I_2 = \int e^{ax}\sin(bx) dx = \frac{e^{ax}}{a^2 + b^2}(a\sin(bx) - b\cos(bx)) + C \end{array} \right.$$

第三种应用情形为形如 $\displaystyle I_n = \int f^n(x) dx$ 的不定积分，通过分部积分后能够对 $f^n(x)$ 进行降次，产生 $\displaystyle I_{n-1} = \int f^{n-1}(x) dx$，从而可以建立 $I_n$ 的递推关系式，求解原不定积分。

例9. 求 $\displaystyle I_n = \int \frac{1}{(x^2 + a^2)^n} dx$，其中 $a \neq 0, n > 1 \in \mathbb{Z}$

$$\begin{array}{ll} \displaystyle \boxed{I_n} = \int \frac{1}{(x^2 + a^2)^n} dx &= \displaystyle x \frac{1}{(x^2 + a^2)^n} - \int x d\frac{1}{(x^2 + a^2)^n} \\ &= \displaystyle x \frac{1}{(x^2 + a^2)^n} - \int x (-n) \frac{1}{(x^2 + a^2)^{n + 1}} 2x dx \\ &= \displaystyle x \frac{1}{(x^2 + a^2)^n} + 2n \int \frac{x^2}{(x^2 + a^2)^{n + 1}} dx \\ &= \displaystyle x \frac{1}{(x^2 + a^2)^n} + 2n \int \frac{x^2 + a^2 - a^2}{(x^2 + a^2)^{n + 1}} dx \\ &= \displaystyle x \frac{1}{(x^2 + a^2)^n} + 2n \int \frac{1}{(x^2 + a^2)^n} dx + 2n \int \frac{- a^2}{(x^2 + a^2)^{n + 1}} \\ & \boxed{= \displaystyle x \frac{1}{(x^2 + a^2)^n} + 2n I_n - 2a^2 n I_{n + 1}} \end{array}$$

将被框起等式两边的所有 $n$ 都替换为 $n - 1$ 并进行化简，可以得到以下递推式：

$$I_n = \frac{x}{2(n - 1)a^2(x^2 + a^2)^{n - 1}} + \frac{2n - 3}{2(n - 1)a^2} I_{n - 1}$$

考虑初始情况 $\displaystyle I_1 = \int \frac{1}{x^2 + a^2}dx$：

$$\begin{array}{ll} \displaystyle \int \frac{1}{x^2 + a^2}dx &= \displaystyle \int \frac{1}{a^2} \frac{1}{(\frac{x}{a})^2 + 1}dx \\ &= \displaystyle \frac{1}{a} \int \frac{1}{(\frac{x}{a})^2 + 1}d\frac{x}{a} \\ &= \displaystyle \frac{1}{a} \arctan \frac{x}{a} + C \end{array}$$

则原不定积分可由以下递归式计算：

$$\left\{ \begin{array}{l} \displaystyle I_1 = \frac{1}{a} \arctan \frac{x}{a} + C \\ \displaystyle I_n = \frac{x}{2(n - 1)a^2(x^2 + a^2)^{n - 1}} + \frac{2n - 3}{2(n - 1)a^2} I_{n - 1} & (n \geq 2) \end{array} \right.$$

这个不定积分的重要性在于，所有形如 $\displaystyle \int \frac{1}{(x^2 + px + q)^n}dx$ 的不定积分都可以通过配方法转化为这个形式，而这是求解有理函数的不定积分通法的基石（之一）。

常见类型的不定积分

有理函数的不定积分

所有的有理函数 $\displaystyle \frac{P_n(x)}{Q_m(x)}$ 都可以通过长除法化为多项式与有理真分式之和，有理真分式是指分子次数小于分母次数（即 $n < m$）的有理函数。

一切的多项式 $Q_m(x) = a_m x^m + a_{m-1}x^{m-1} + \dots + a_0$ 都能够在实数域内作因式分解，将其分解为下面的形式：

$$Q_m(x) = a_m (x - \alpha)^{r_\alpha} \dots (x - \omega)^{r_\omega} (x^2 + p x + q)^s \dots (x^2 + ux + v)^{t}$$

而所有的既约有理真分式 $\displaystyle \frac{P_n(x)}{Q_m(x)}$ （分母 $Q_m(x)$ 的最高次项系数 $a_m = 1$）又可以唯一地分解为以下分式之和：

$$\begin{array}{rl} \displaystyle \frac{P_n(x)}{Q_m(x)} &= \displaystyle \frac{A_1}{x - \alpha} + \frac{A_2}{(x - \alpha)^2} + \dots + \frac{A_{r_\alpha}}{(x - \alpha)^{r_\alpha}} \\ &+ \dots \\ &+ \displaystyle \frac{O_1}{x - \omega} + \frac{O_2}{(x - \omega)^2} + \dots + \frac{O_{r_\omega}}{(x - \omega)^{r_\omega}} \\ &+ \displaystyle \frac{P_1 x + Q_1}{x^2 + p x + q} + \frac{P_2 x + Q_2}{(x^2 + p x + q)^2} + \dots + \frac{P_s x + Q_s}{(x^2 + p x + q)^s} \\ &+ \dots \\ &+ \displaystyle \frac{U_1 x + V_1}{x^2 + u x + v} + \frac{U_2 x + V_2}{(x^2 + u x + v)^2} + \dots + \frac{U_t x + V_t}{(x^2 + u x + v)^t} \end{array}$$

通过待定系数法，或代入特殊值解线性方程组的方法我们可以确定上式中的所有由大写字母表示的变量 $A_1, A_2, ..., U_t, V_t$。

这样，我们只需要能够计算以下两个基本的不定积分，就能够计算所有的有理函数的不定积分。

$$\begin{array}{c} \displaystyle I_1 = \int \frac{1}{(x - a)^n} dx & \displaystyle I_2 = \int \frac{Ax + B}{(x^2 + px + q)^n}dx \end{array}$$

下面将给出这两个积分的计算。

$$\begin{array}{ll} \displaystyle I_1 = \int \frac{1}{(x - a)^n} dx &= \displaystyle \int \frac{1}{(x - a)^n} d(x - a) \\ &= \left\{ \begin{array}{l} \displaystyle \ln |x - a| + C & (n = 1) \\ \displaystyle \frac{1}{(1 - n)(x - a)^{n - 1}} + C & (n \geq 2) \end{array} \right. \end{array}$$

$$\begin{array}{ll} \displaystyle I_2 = \int \frac{Ax + B}{(x^2 + px + q)^n}dx &= \displaystyle \frac{Ax}{(x^2 + px + q)^n}dx + \frac{B}{(x^2 + px + q)^n}dx \\ &= \displaystyle \int \frac{\frac{A}{2}(2x + p) - \frac{Ap}{2}}{(x^2 + px + q)^n}dx + \int \frac{B}{(x^2 + px + q)^n}dx \\ &= \displaystyle \int \frac{\frac{A}{2}(2x + p)}{(x^2 + px + q)^n}dx - \int \frac{\frac{Ap}{2}}{(x^2 + px + q)^n}dx + \int \frac{B}{(x^2 + px + q)^n}dx \\ &= \displaystyle \frac{A}{2} \int \frac{d(x^2 + px + q)}{(x^2 + px + q)^n} + \frac{2B - Ap}{2}\int \frac{1}{(x^2 + px + q)^n}dx \\ &= \displaystyle \frac{A}{2} \int \frac{d(x^2 + px + q)}{(x^2 + px + q)^n} + \frac{2B - Ap}{2}\int \frac{1}{[(x + \frac{p}{2})^2 + (q - \frac{p^2}{4})]^n}dx \\ &= \displaystyle \frac{A}{2} \boxed{\int \frac{d(x^2 + px + q)}{(x^2 + px + q)^n}} + \frac{2B - Ap}{2}\boxed{\int \frac{1}{[(x + \frac{p}{2})^2 + (\sqrt{\frac{4q - p^2}{2}})^2]^n}dx} \end{array}$$

上面框起的两个不定积分都是我们已经计算过的。

$$\begin{array}{rl} \displaystyle \boxed{\int \frac{d(x^2 + px + q)}{(x^2 + px + q)^n}} &= \left\{ \begin{array}{l} \displaystyle \ln |x^2 + px + q| + C & (n = 1) \\ \displaystyle \frac{1}{(1 - n)(x^2 + px + q)^{n - 1}} + C & (n \geq 2) \end{array} \right. \\ \boxed{\int \frac{1}{[(x + \frac{p}{2})^2 + (\sqrt{\frac{4q - p^2}{2}})^2]^n}dx} &= \left\{ \begin{array}{l} \displaystyle \frac{1}{\sqrt{\frac{4q - p^2}{2}}} \arctan \frac{x + \frac{p}{2}}{\sqrt{\frac{4q - p^2}{2}}} + C & (n = 1) \\ \displaystyle \small{I_n = \frac{x}{(n - 1)(4q - p^2) (x^2 + \frac{4q - p^2}{2})^{n - 1}} + \frac{2n - 3}{(n - 1) (4q - p^2)} I_{n - 1}} & (n \geq 2) \end{array} \right. \end{array}$$

需要注意的是，虽然我们能够通过这个方法求解一切有理函数的不定积分，然而计算过程是十分复杂的，如果存在其他手段能够计算某个有理函数的不定积分，需要慎重考虑使用这个方法。

三角有理式的不定积分

由 $u_1(x), u_2(x), \dots, u_k(x)$ 以及常数经过有限次四则运算得到的函数称为关于 $u_1(x), u_2(x), \dots, u_k(x)$ 的有理式，用 $R(u_1(x), u_2(x), \dots, u_k(x))$ 表示。

对于不定积分 $\displaystyle \int R(\sin x, \cos x, \dots, \csc x) dx$ 通过换元 $\displaystyle t = \tan \frac{x}{2}$ （其中 $x \in (-\pi, \pi)$）即可将三角有理式转化为有理函数。这是因为三角函数的万能公式：

以及反正切函数的微分：

$$\begin{array}{c} \displaystyle t = \tan \frac{x}{2} & \Leftrightarrow & \displaystyle x = 2 \arctan t & , & x \in (-\pi, \pi) \end{array} \\ \begin{array}{c} \displaystyle dx = d(2 \arctan t) = \frac{2dt}{1 + t^2} \end{array}$$

然而，计算有理函数的不定积分通常是复杂的，对于某些特定形式的三角有理式的积分，有一些其他方法可以简便地进行计算。下面列举苏德矿微积分中列出的几种常见情况及其解法。

$\displaystyle \int \sin^n x \cos^m x dx$ 型，其中 $n,m$ 至少有一个奇数

通过三角恒等式 $\sin^2 x + \cos^2 x = 1$ 以及凑微分即可将被积函数化为仅含单一三角函数的函数。

$\displaystyle \int \sin^n x \cos^m x dx$ 型，其中 $n,m$ 均是偶数

通过三角函数的二倍角公式降幂，化为上面的情形。

$\displaystyle \int \sin nx \cos mx dx$ 型

被积分函数中的 $\sin,\cos$ 可以随意排列组合，使用积化和差公式拆分为两个仅含单一三角函数的函数之不定积分。

$\displaystyle \int R(\sin^2 x, \cos^2 x, \sin x\cos x)dx$ 型

令 $\tan x = t$，则有：

$$\begin{array}{rl} \displaystyle dx &= \displaystyle d\arctan x = \frac{1}{1 + t^2}dt \\ \displaystyle \sin^2 x &= \displaystyle \frac{\sin^2 x}{\cos^2 x} \cos^2 x = \frac{t^2}{1 + t^2} \\ \displaystyle \cos^2 x &= \displaystyle \frac{1}{\sec^2 x} = \frac{1}{1 + t^2} \\ \displaystyle \sin x\cos x &= \displaystyle \frac{1}{2}\sin 2x = \frac{t}{1 + t^2} \\ \displaystyle \int R(\sin^2 x, \cos^2 x, \sin x\cos x)dx &= \displaystyle \int R(\frac{t^2}{1 + t^2}, \frac{1}{1 + t^2}, \frac{t}{1 + t^2}) \frac{1}{1 + t^2}dt \end{array}$$

$\displaystyle \int \frac{a\sin x + b\cos x}{c\sin x + d\cos x} dx$ 型

待定系数法，令：

$$\int \frac{A(c \cos x - d \sin x) + B(c\sin x + d\cos x)}{c\sin x + d\cos x} dx = \int \frac{a\sin x + b\cos x}{c\sin x + d\cos x} dx$$

而等式左边的积分是易于计算的：

$$\begin{array}{ll} \displaystyle L.H.S. &= \displaystyle \int \frac{A(c \cos x - d \sin x) + B(c\sin x + d\cos x)}{c\sin x + d\cos x} dx \\ &= \displaystyle A \int \frac{c \cos x - d \sin x}{c\sin x + d\cos x} dx + B \int \frac{c\sin x + d\cos x}{c\sin x + d\cos x} dx \\ &= \displaystyle A \int \frac{d(c\sin x + d\cos x)}{c\sin x + d\cos x} + Bx + C \\ &= \displaystyle A \ln |c\sin x + d\cos x| + Bx + C \end{array}$$

不常见的特殊类型不定积分

分段函数的不定积分

我们已经讨论过，不定积分是原函数的反导数，这就意味着原函数必定是连续的。在原函数存在的情况下，不定积分可以由以下方法计算： - 在分段的区间内分别求不定积分，然后考虑原函数的连续性 - 利用变限积分进行计算

例10. 求 $\displaystyle I = \int e^{|x|} dx$

由于：

$$\displaystyle e^{|x|} = \left\{ \begin{array}{l} \displaystyle e^{-x} & (x < 0) \\ \displaystyle e^{x} & (x \geq 0) \end{array} \right.$$

在两个区间内分别积分：

$$I = F(x) = \displaystyle \int e^{|x|} dx = \left\{ \begin{array}{l} \displaystyle \int e^{-x} dx & (x < 0) \\ \displaystyle \int e^{x} dx & (x \geq 0) \end{array} \right. = \left\{ \begin{array}{l} \displaystyle -e^{-x} + C_1 & (x < 0) \\ \displaystyle e^x + C_2 & (x \geq 0) \end{array} \right.$$

考虑原函数的连续性，有：

$$\begin{array}{ll} \left\{ \begin{array}{l} \displaystyle \lim_{x\rightarrow 0^-} F(x) = F(0) \\ \displaystyle \lim_{x\rightarrow 0^+} F(x) = F(0) \\ \end{array} \right. &\Rightarrow \left\{ \begin{array}{l} \displaystyle \lim_{x\rightarrow 0^-} (-e^{-x} + C_1) = 1 + C_2 \\ \displaystyle \lim_{x\rightarrow 0^+} (e^x + C_2) = 1 + C_2 \\ \end{array} \right. \\ &\Rightarrow \left\{ \begin{array}{l} \displaystyle -1 + C_1 = 1 + C_2 \\ \displaystyle 1 + C_2 = 1 + C_2 \\ \end{array} \right. \\&\Rightarrow C_2 = -2 + C_1 \end{array}$$

综上：

$$I = \int e^{|x|} dx = \left\{ \begin{array}{l} \displaystyle -e^{-x} + C & (x < 0) \\ \displaystyle e^x + -2 + C & (x \geq 0) \end{array} \right.$$

除此之外，可以利用变限积分计算这个不定积分：注意到 $e^{|x|}$ 是一个连续函数，因此，一定存在一个原函数 $\displaystyle F(x) = \int_0^x e^{|t|} dt$，只需要计算这个变上限积分即可得到原不定积分 $I = F(x) + C$。

$$I = F(x) + C = \left\{ \begin{array}{l} \displaystyle \int_0^x e^{-t} dt & (t < 0) \\ \displaystyle \int_0^x e^t dt & (t \geq 0) \end{array} \right. + C = \left\{ \begin{array}{l} \displaystyle e^x - 1 & (t < 0) \\ \displaystyle 1 - e^{-x} & (t \geq 0) \end{array} \right. + C$$