一元函数的导数

本文详细讨论了一元函数的导数及其应用。首先介绍了函数的连续性，定义了左连续、右连续和间断点等概念。接着，阐述了导数与微分的定义，解释了导数的几何意义和微分的形式不变性。随后，介绍了导数的计算方法，包括基本初等函数的导数、有理运算和复合运算的导数、隐函数和反函数的导数等。文章还探讨了导数的应用，如极值点、凹凸性、曲率等，并提供了相关定理的证明和实例。通过本文，读者可以全面掌握一元函数导数的基本理论和计算技巧。

（摘要由 OpenAI GPT 4o 生成）

函数的连续性

函数 \(f(x)\) 在 \(x = x_0\) 处的连续性按以下法则定义：

• 若 \(\displaystyle \lim_{x \rightarrow x_0^-} f(x) = f(x_0)\) 则称函数 \(f(x)\) 在 \(x = x_0\) 处左连续。

• 若 \(\displaystyle \lim_{x \rightarrow x_0^+} f(x) = f(x_0)\) 则称函数 \(f(x)\) 在 \(x = x_0\) 处右连续。

• 若 \(\displaystyle \lim_{x \rightarrow x_0} f(x) = f(x_0)\) 则称函数 \(f(x)\) 在 \(x = x_0\) 处连续。

• 函数 \(f(x)\) 在 \(x = x_0\) 处连续当且仅当函数 \(f(x)\) 在 \(x = x_0\) 处左连续且右连续。

如果函数 \(f(x)\) 在 \(U^o(x_0)\) 有定义，而在 \(x_0\) 不连续，则称 \(x_0\) 为函数 \(f(x)\) 的一个间断点。 根据函数 \(f(x)\) 在 \(x_0\) 处的左右极限的存在性与极限值，间断点可以分类为可去间断点\(^{(I)}\)、跳跃间断点\(^{(I)}\)、无穷间断点\(^{(II)}\)和振荡间断点\(^{(II)}\)。

初等函数及由初等函数进行有限次四则运算及复合得到的函数在其定义区间内必然连续。

有限闭区间上连续函数满足介值定理、最值定理与零点定理。

介值定理 若 \(f(x)\) 在 \([a,b]\) 上连续，且 \(f(a) \neq f(b)\)，则对任意的 \(f(a)\) 与 \(f(b)\) 之间的值 \(C\)，均存在至少一个 \(\xi \in [a,b]\) 使得 \(f(\xi) = C\)。

最值定理 若 \(f(x)\) 在 \([a,b]\) 上连续，则 \(f(x)\) 在 \([a,b]\) 上存在最大值 \(M\) 和最小值 \(m\)。

由介值定理与最值定理，可以得到推论： \(f(x)\) 在 \([a,b]\) 上连续，则 \(f(x)\) 在 \([a,b]\) 上可以取到任何一个介于其最大值与最小值之间的函数值。

零点定理 若 \(f(x)\) 在 \([a,b]\) 上连续，且 \(f(a) \cdot f(b) < 0\)，则至少存在一个 \(\xi \in [a,b]\) 使得 \(f(\xi) = 0\)。 零点定理是上面的推论的一个特例。

导数与微分的定义

导数与微分的定义

\[ f'(x_0) = \lim_{\Delta x \rightarrow 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} = \lim_{x \rightarrow x_0} \frac{f(x) - f(x_0)}{x - x_0} \]

根据此式，细分极限为左极限与右极限，可以得到单侧导数（左导数、右导数）的定义。

函数 \(f(x)\) 在 \(x_0\) 可导，取决于上面的极限是否存在。函数 \(f(x)\) 在 \(x_0\) 可导，当且仅当函数 \(f(x)\) 在 \(x_0\) 左可导并且右可导。

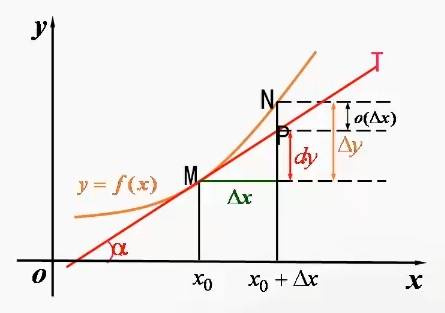
若 \(\Delta y = f(x_0 + \Delta x) - f(x_0) = A \cdot \Delta x + \omicron(\Delta x)\)，称函数 \(f(x)\) 在 \(x_0\) 可微，\(A \cdot \Delta x\) 为该点的微分，用记号 \(dy\) 表示。

事实上，这是一种尝试线性近似函数变化的方法，这里的线性主部 \(A\) 就是 \(f(x)\) 在 \(x_0\) 的导数值。即 \(dy = A \cdot \Delta x = f'(x_0) \cdot \Delta x\)。

而又由于当 \(f(x) = x\) 时，对任意一点 \(x_0\) 都有 \(dy = \Delta x\)，这样，我们有 \(dy = d(x) = \Delta x\)，因此上面的式子也可以写成更为熟知的形式：

\[ dy = f'(x_0) \cdot dx \]

函数 \(f(x)\) 在某点 \(x_0\) 的导数之几何意义为函数 \(f(x)\) 在某点 \(x_0\) 处切线的斜率，而函数 \(f(x)\) 在某点 \(x_0\) 的微分则代表函数 \(f(x)\) 在某点 \(x_0\) 处切线上的增量，高阶无穷小量 \(\omicron(\Delta x)\) 则是其函数值增量与函数 \(f(x)\) 在某点 \(x_0\) 处切线上的增量之差。如下图所示。

可导一定连续、连续不一定可导

可导一定连续 利用导数的定义式 \(\displaystyle f'(x_0) = \lim_{x \rightarrow x_0} \frac{f(x) - f(x_0)}{x - x_0}\) 以及极限的四则运算法则之推论即可得证。

连续不一定可导 常见的反例如 \(f(x) = |x|\) 在 \(x = 0\) 连续却不可导。事实上，对于含有绝对值因子的函数在零点的导数是否存在取决于其左右极限是否相等且为 0，这将在后面加以论述。

往往需要考察可导函数 \(f(x)\) 之导函数在某点的极限值，形如 \(\displaystyle \lim_{x \rightarrow 0}f'(x)\)，然而，函数 \(f(x)\) 可导不能推出其导函数 \(f'(x)\) 处处连续，甚至无法推出其导函数处处存在极限。经典的反例如下式所示：

\[ f(x) = \left\{ \begin{array}{lcl} \displaystyle x^2 \sin \frac{1}{x} & , & x \neq 0 \\ 0 & , & x = 0 \end{array} \right. \]

\(f(x)\) 处处可导，然而 \(\displaystyle \lim_{x \rightarrow 0}f'(x)\) 却不存在。

因此，对于与导数有关的极限在使用洛必达法则时，较为稳妥的策略是： 若 \(f(x),\ g(x)\) 满足 \(n\) 阶可导，则至多可以使用 \((n - 1)\) 次洛必达法则。 若 \(f(x),\ g(x)\) 满足 \(n\) 阶连续可导，则至多可以使用 \(n\) 次洛必达法则，这是因为连续可推得函数在某点的极限等于函数在某点的函数值。

上面的结论是基于洛必达后极限需要存在的要求，以及函数连续时，可以直接利用 \(\displaystyle \lim_{x\rightarrow x_0}f(x) = f(x_0)\) 求极限的性质。然而上面的两个结论并非在所有情况下一定是最恰当的，它实际上缩小了洛必达的可用范围。

可导函数的导函数不一定连续 最著名的例子是下面的反例，在这个例子中，\(f(x)\) 处处可导，而 \(\displaystyle \lim_{x \rightarrow 0}f'(x)\) 不存在，自然 \(f'(x)\) 在 \(x = 0\) 不连续：

\[ \begin{array}{ccc} f(x) = \left\{ \begin{array}{l} \displaystyle x^2 \sin \frac{1}{x} & (x \neq 0) \\ \displaystyle 0 & (x = 0) \end{array} \right. &,& f'(x) = \left\{ \begin{array}{l} \displaystyle 2x \sin \frac{1}{x} - \cos \frac{1}{x} & (x \neq 0) \\ \displaystyle 0 & (x = 0) \end{array} \right. \end{array} \]

实际上，根据达布定理，如果 \(f\) 是一个可导函数，并且其导数 \(f'\) 不连续，能够造成其导数 \(f'\) 不连续的唯一可能是极限 \(\displaystyle \lim_{x\rightarrow a}f'(x)\) 震荡¹。

判断函数的可导性

TODO

含有绝对值因式的函数在零点的导数

一阶微分的形式不变性

定理 若 \(u = \varphi(x)\) 在点 \(x\) 处可微，\(y = f(u)\) 在点 \(u\)（\(u = \varphi(x)\)）处可微，则复合函数 \(y = f(\varphi(x))\) 在点 \(x\) 处可微，且有：

\[ dy = f'(u)du \]

定理的证明需要用到复合函数的求导法则，不过这并不涉及循环论证。

我更加喜欢下面这个形式，这指出求微分对任何的 \(\bigcirc\) 都能得到相同形式的结果，无论 \(\bigcirc = x\) 还是多么复杂的表达式。

\[ d\ (\text{expr}) = \frac{d}{d\bigcirc}(\text{expr}) d\bigcirc \]

这也是可以对一个等式两边求微分的依据，这个动作要求，至少存在一个 \(\bigcirc\) ，使得等式两边对同一个 \(\bigcirc\) 可微（例如 \(\bigcirc = x\) ）。

对于等式 \(\text{expr}_1 = \text{expr}_2\)，将等式两边都看作 \(\bigcirc\) 的函数，两边对 \(\bigcirc\) 求导，有：

\[ \frac{d}{d\bigcirc}(\text{expr}_1) = \frac{d}{d\bigcirc}(\text{expr}_2) \]

在这个等式的两侧同时乘以无穷小量 \(d\bigcirc\)（或理解为另一个微分），等式变为：

\[ \frac{d}{d\bigcirc}(\text{expr}_1) d\bigcirc = \frac{d}{d\bigcirc}(\text{expr}_2) d\bigcirc \]

根据一阶微分形式不变性，则有：

\[ d(\text{expr}_1) = d(\text{expr}_2) \]

导数的计算

基本初等函数的导函数

\[ \begin{array}{ll} \displaystyle (C)' = 0 & \displaystyle (x^\alpha)' = \alpha x^{\alpha - 1} \\ \displaystyle (a^x)' = a^x \ln a & \displaystyle (e^x)' = e^x \\ \displaystyle (\log_a x)' = \frac{1}{x \ln a} & \displaystyle (\ln |x|)' = \frac{1}{x} \\ \displaystyle (\sin x)' = \cos x & \displaystyle (\cos x)' = - \sin x \\ \displaystyle (\tan x)' = \sec^2 x & \displaystyle (\cot x)' = - \csc^2 x \\ \displaystyle (\sec x)' = \sec x \tan x & \displaystyle (\csc x)' = - \csc x \cot x \\ \displaystyle (\arcsin x)' = \frac{1}{\sqrt{1 - x^2}} & \displaystyle (\arccos x)' = - \frac{1}{\sqrt{1 - x^2}} \\ \displaystyle (\arctan x)' = \frac{1}{1 + x^2} & \displaystyle (\text{arccot } x)' = - \frac{1}{1 + x^2} \end{array} \]

有理运算、复合运算的导函数

\[ \begin{array}{ll} \displaystyle (u \pm v)' = uv & \\ \displaystyle (u \cdot v)' = u'v + v'u & \displaystyle (\frac{u}{v})' = \frac{u'v - v'u}{v^2} \\ \displaystyle \frac{dz}{dx} = \frac{dz}{dy} \cdot \frac{dy}{dx} & \displaystyle \{f[\varphi(x)]\}' = f'[\varphi(x)] \cdot \varphi'(x) \end{array} \]

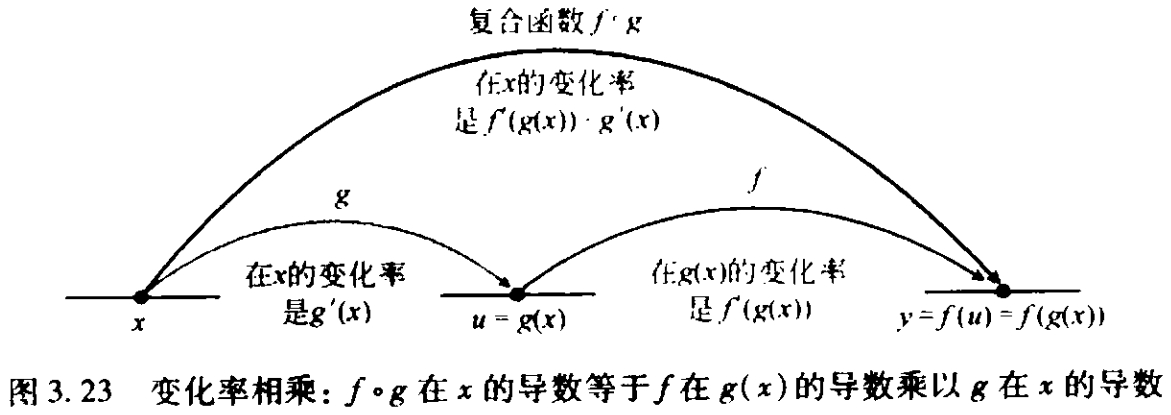
链式法则 \(\displaystyle \frac{dz}{dx} = \frac{dz}{dy} \cdot \frac{dy}{dx}\)

实际上，该法则可以看作是函数关系图中，\(z\) 到 \(x\) 的所有路径的「每一段路径两端点微分之比」乘积之和。只是在一元的这种情况中，只存在一条路径 \(z \rightarrow y \rightarrow x\)。

下图²所示为一元情况下的链式法则和推广到多元情况下的链式法则。

需要注意的是，复合函数的其中一个成分（或两个成分）在某点导数不存在不能说明复合函数在某点的导数不存在，只是这种情况无法使用链式法则求导。一个十分简单的例子是 \(f(x) = x^2\)，\(\varphi(x) = |x|\)，则 \(f[\varphi(x)] = x^2\)，其导数处处存在。

隐函数、反函数、由参数方程定义的函数的导函数

隐函数求导法则

若方程 \(F(x,y) = 0\) 确定 \(y\) 与 \(x\) 的函数关系式，则有：

\[ \frac{dy}{dx} = -\frac{F'_x}{F'_y} \]

上面的公式通过多元函数的全微分可以得到说明：

\[ \displaystyle dF = \frac{\partial F}{\partial x} dx + \frac{\partial F}{\partial y} dy \Rightarrow 0 = \frac{\partial F}{\partial x} dx + \frac{\partial F}{\partial y} dy \Rightarrow \frac{dy}{dx} = -\frac{F'_x}{F'_y} \]

对于确定的 \(F\)，通常通过对方程 \(F(x,y) = 0\) 两边微分（使用算子 \(\displaystyle \frac{d}{dx}\)），然后展开 \(\displaystyle \frac{dF}{dx}\) 求解关于 \(\displaystyle \frac{dy}{dx}\) 的方程得到 \(\displaystyle \frac{dy}{dx}\) ，必须始终牢记，在这里 \(y\) 是 \(x\) 的函数而非自由变量。

TODO

为什么上面的 \(dF = 0\)？是否存在循环论证？

反函数求导法则

若 \(x = \varphi (y)\) 在某区间单调可导，并且其导函数 \(\varphi'(y) \neq 0\)，则其反函数 \(y = \varphi^{-1}(x)\) 也可导，其导函数为：

\[ \begin{array}{ll} \displaystyle (\varphi^{-1})'(x) = \frac{1}{\varphi'(x)} & \displaystyle \frac{dy}{dx} = \frac{1}{\frac{dx}{dy}} \end{array} \]

实际上就是 \((\mathbb{R \rightarrow R}) \rightarrow (\mathbb{R \rightarrow R})\) 的两个算子 \('\) 与 \(^{-1}\) 可交换。

参数方程定义的函数的求导法则

设 \(y = f(x)\) 由参数方程 \(x = \varphi (t)\)，\(y = \psi (t)\) 确定，并且 \(\varphi'(t) \neq 0\)，则有：

\[ \displaystyle \frac{dy}{dx} = \frac{\psi'(t)}{\varphi'(t)} \]

这个公式可以通过对方程组 \(x = \varphi (t)\)，\(y = \psi (t)\) 两边使用微分算子 \(d\) 得到：

\[ \left\{ \begin{array}{l} \displaystyle dx = d\varphi (t) \\ \displaystyle dy = d\psi (t) \end{array} \right. \Rightarrow \left\{ \begin{array}{l} \displaystyle dx = \varphi'(t)dt \\ \displaystyle dy = \psi'(t)dt \end{array} \right. \Rightarrow \displaystyle \frac{dy}{dx} = \frac{\psi'(t)}{\varphi'(t)} \]

高阶导数、牛顿莱布尼茨公式

牛顿莱布尼茨公式是导数的乘法法则在高阶导数上的推广：

\[ (uv)^{(n)} = \sum_{k = 0}^{n}C_n^k u^{(k)} v^{(n - k)} \]

这在形式上与二项式 \((u + v)^n\) 的二项式展开一致。

根据导数的加减法法则，不难得到：

\[ (u \pm v)^{(n)} = u^{(n)} \pm v^{(n)} \]

对于求高阶导数的题目，一般方法是归纳法（可能需要适当拆分）或将函数拆分成熟知泰勒级数的函数，从而写出该函数的泰勒展开式以求出某点的导函数值。

对数求导法

对于幂指函数、连乘或连除构成的函数，可以使用对数求导法：两端求自然对数，然后根据隐函数求导法求出 \(\displaystyle \frac{dy}{dx}\)。

根据某点导数求极限、根据极限求某点导数

简而言之，凑某点导数的定义。

当 \(\bigcirc \rightarrow 0\)（代数式 \(\bigcirc\) 需要能够同时满足 \(\bigcirc \rightarrow 0^+\) 以及 \(\bigcirc \rightarrow 0^-\)），并且在某个去心邻域 \(U^o(x_0)\) 内 \(\bigcirc \neq 0\)，则有：

\[ f'(x_0) = \lim_{\bigcirc \rightarrow 0} \frac{f(x_0 + \bigcirc) - f(x_0)}{\bigcirc} = \lim_{x \rightarrow x_0} \frac{f(x_0 + \bigcirc) - f(x_0)}{\bigcirc} \]

关于对代数式 \(\bigcirc\) 的限制，一个经典的错误使用情形是当 \(x \rightarrow 0\) 时的 \(\displaystyle \bigcirc = \sin\frac{1}{x}\)，因为对于 \(\displaystyle \sin\frac{1}{x}\)，在零的任意一个去心邻域，总是能找到 \(k \in \mathbb{Z}^\star\) 使得其零点 \(\displaystyle x = \frac{1}{k\pi}\) 落在这个邻域内。

另外一个经典的错误使用情形是 \(\displaystyle \bigcirc = |x|\)，因为 \(|x|\) 并不能够 \(\rightarrow 0^-\)。

微分中值定理

微分中值定理建立函数与一阶导数间的联系，对于含有拉格朗日余项的泰勒展开，则是建立函数与高阶导数间的联系。

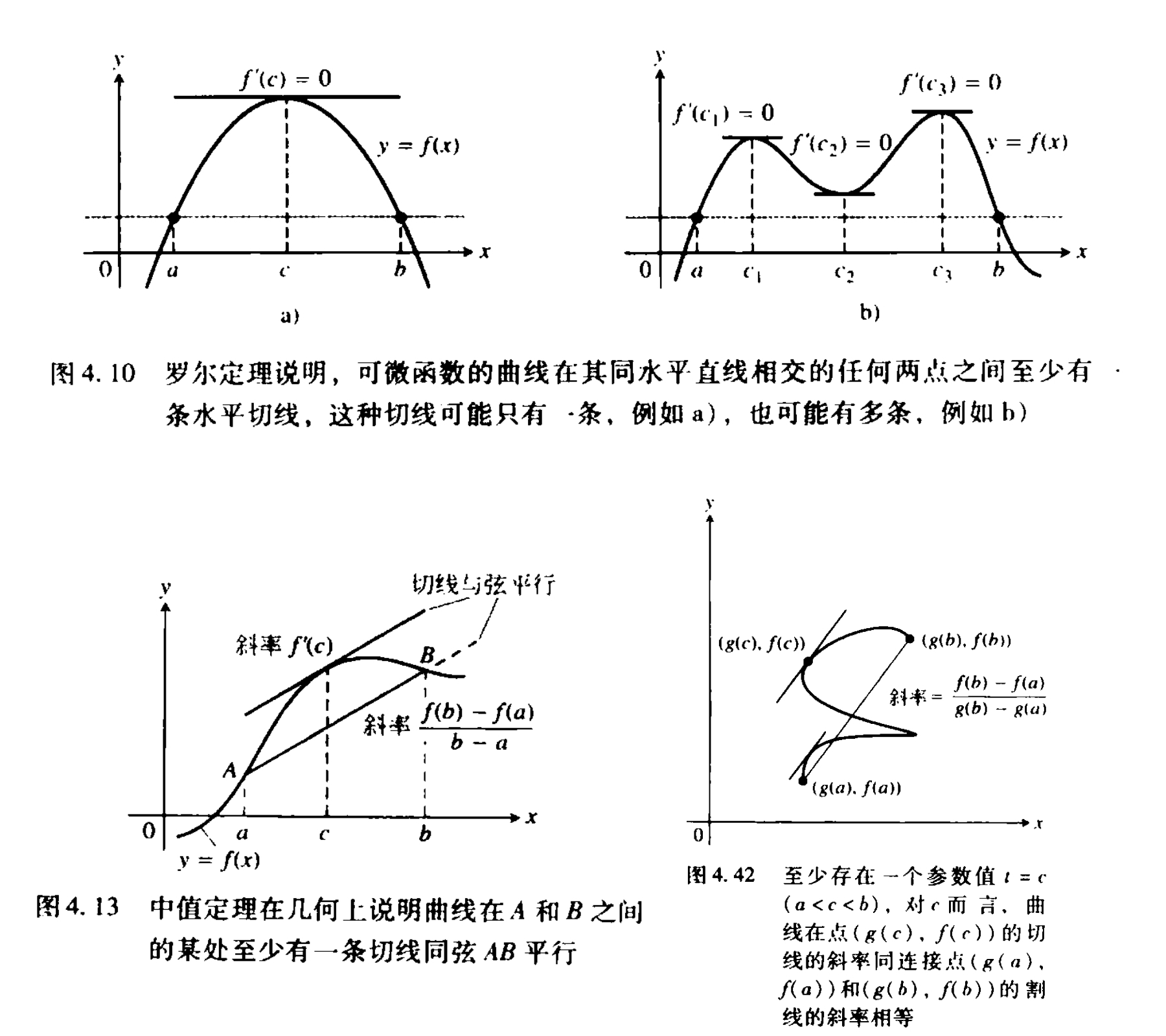
三个微分中值定理的几何图示如下图³所示。

罗尔定理 如果函数 \(f(x)\) 在闭区间 \([a,b]\) 连续，在开区间 \((a,b)\) 可导，并且 \(f(a) = f(b)\)，则至少存在一点 \(\xi \in (a,b)\) 使得 \(f'(\xi) = 0\)。

罗尔定理的证明可以考察函数 \(f(x)\) 在闭区间 \([a,b]\) 内的绝对极大值和绝对极小值（最大值与最小值），这两种极值只可能出现在 \(f'(x_0) = 0\) 的内点，或是两个端点 \(f(a)\) 与 \(f(b)\)，针对这两种情况分类讨论即可。

罗尔定理说明可导的平面曲线在两个不同点穿过同一条水平直线，则在这两点之间，必然存在一点，在这一点处曲线的切线也是水平的。

罗尔定理的一个物理上的例子是，往返跑必然存在某一个时刻，在这个时刻的瞬时速度为零。

罗尔定理常常被用于讨论方程 \(f(x) = 0\) 实数根的个数，在这种情况下，我们对 \(f(x)\) 的任意一个原函数使用罗尔定理。

在讨论方程 \(f(x) = 0\) 根的个数的时候，下面的一个罗尔定理的推论往往十分有用。

推论 如果函数 \(f(x)\) 在区间 \(I\) （有限、无限、开、闭）内，满足 \(f^{(n)}(x) \neq 0\)，则函数 \(f(x)\) 在区间 \(I\) 至多有 \(n\) 个零点。

我们使用反证法并迭代地使用罗尔定理即可证明上面的推论。

推广罗尔定理，令 \(\displaystyle h(x) = f(x) - [f(a) + \frac{f(b) - f(a)}{b - a}(x - a)]\) （这个函数的构造是取函数 \(f(x)\) 的两端点之连线，将其与函数 \(f(x)\) 作差），对 \(h(x)\) 使用罗尔定理，可以得到拉格朗日中值定理。

拉格朗日中值定理 如果函数 \(f(x)\) 在闭区间 \([a,b]\) 连续，在开区间 \((a,b)\) 可导，那么至少存在一点 \(\xi \in (a,b)\) 使得 \(\displaystyle f'(\xi) = \frac{f(b) - f(a)}{b - a}\)。

拉格朗日中值定理说明在区间内必然存在某点的瞬时变化量等于平面曲线在区间内的平均变化量，它是倾斜情况下的罗尔定理。

推广拉格朗日中值定理，可以得到柯西中值定理。柯西中值定理是证明洛必达定理的重要基础。

柯西中值定理 如果函数 \(f(x)\) 与函数 \(g(x)\) 在闭区间 \([a,b]\) 连续，在开区间 \((a,b)\) 可导，并且在整个开区间 \((a,b)\) 内，函数 \(g(x) \neq 0\)，那么至少存在一点 \(\xi \in (a,b)\) 使得 \(\displaystyle \frac{f'(\xi)}{g'(\xi)} = \frac{f(b) - f(a)}{g(b) - g(a)}\)。

证明柯西中值定理需要应用两次拉格朗日中值定理。

其中一次用于论述等式右侧的分母 \(g(b) - g(a) \neq 0\)，另一次对函数 \(\displaystyle F(x) = f(x) - \{f(a) + \frac{f(b) - f(a)}{g(b) - g(a)}[g(x) - g(a)]\}\) 应用拉格朗日中值定理，这个函数的构造可以参考如何运用罗尔定理证明拉格朗日中值定理，我们可以将函数 \(g(x)\) 类比为特殊的 \(x\) 轴。

含有拉格朗日余项的泰勒展开（泰勒中值定理） 如果函数 \(f(x)\) 在开区间 \((a,b)\) \((n+1)\) 阶可导，对于任意的 \(x_0 \in (a,b)\)，至少存在一个 \(\xi \in (a,b)\) 使得下面的等式成立。

\[ f(x) = f(x_0) + f'(x_0)(x - x_0) + \frac{f''(x_0)}{2!}(x - x_0)^2 + \cdots + \frac{f^{(n)}(x_0)}{n!}(x - x_0)^n + R_n(x) \]

\[ R_n(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!}(x - x_0)^{n+1} \]

其中 \(R_n(x)\) 被称为拉格朗日余项。

含有拉格朗日余项的泰勒展开也可以视作对拉格朗日中值定理在高阶导数上的推广。对于拉格朗日中值定理所生成的 \(f'(\xi_1)\)，再次使用拉格朗日中值定理的变形 \(f(x) = f(x_0) + f'(\xi)(x - x_0)\) 展开 \(f'(\xi_1)\)，生成 \(f''(\xi_2)\)，反复迭代这个过程，即可得到含拉格朗日余项的泰勒展开。

含有皮亚诺余项的泰勒展开 如果函数 \(f(x)\) 在开区间 \((a,b)\) \(n\) 阶可导，则有下面的等式成立：

\[ f(x) = f(x_0) + \sum_{k = 1}^{n}\frac{f^{(k)}(x_0) \cdot (x - x_0)^k}{k!} + o[(x - x_0)^n] \]

特别地，当 \(x_0 = 0\)，称此展开式为麦克劳林展开。

当 \(n \rightarrow \infty\)，称此展开式（此时没有最后的皮亚诺余项）为泰勒级数（麦克劳林级数）。

由上面的展开式，我们可以得到这样的结论：

(1) \(n\) 阶可导的奇函数在零点处的偶数阶导函数值 \(f^{(2k)}(0) = 0\)，如果它是\(x \rightarrow 0\) 时的无穷小量，它的无穷小阶数必然为奇数阶；

(2) \(n\) 阶可导的偶函数在零点处的奇数阶导函数值 \(f^{(2k + 1)}(0) = 0\)，如果它是\(x \rightarrow 0\) 时的无穷小量，它的无穷小阶数必然为偶数阶。

导数的应用

驻点、极值点、最值点

如果存在 \(x_0\) 的邻域 \(U(x_0, \delta)\)，在这个邻域内，对于任意的 \(x\)，都有： - \(f(x) \geq f(x_0)\)，则称 \((x_0, f(x_0))\) 是 \(f(x)\) 的一个极小值点。 - \(f(x) \leq f(x_0)\)，则称 \((x_0, f(x_0))\) 是 \(f(x)\) 的一个极大值点。

如果有 \(f'(x_0) = 0\)，则称 \((x_0, f(x_0))\) 是 \(f(x)\) 的一个驻点。

极值点不一定是驻点，例如 \(f(x) = |x|\) 的极值点 \((0,0)\)。

驻点也不一定是极值点，例如 \(f(x) = x^3\) 的驻点 \((0,0)\)。

所有可能的极值点是所有导数为零的点以及所有导数不存在的点。

极值点的充分条件有以下三条：

极值点的第一充分条件 设 \(f'(x_0) = 0\) （或者 \(f(x)\) 在 \(x_0\) 处连续），且在 \(x_0\) 的某个去心邻域 \(U^o(x_0, \delta)\) 可导，若： - 当 \(x \in (x_0 - \delta, x_0)\) 时 \(f'(x_0) < 0\)，并且当 \(x \in (x_0 - \delta, x_0)\) 时 \(f'(x_0) > 0\)，则 \(f(x)\) 在 \(x_0\) 取极小值。 - 当 \(x \in (x_0 - \delta, x_0)\) 时 \(f'(x_0) > 0\)，并且当 \(x \in (x_0 - \delta, x_0)\) 时 \(f'(x_0) < 0\)，则 \(f(x)\) 在 \(x_0\) 取极大值。 - 在去心邻域内 \(x_0\) 的两侧 \(f'(x)\) 不变号，则 \(f(x)\) 在 \(x_0\) 处没有极值。

可以考虑 \(f(x) = |x|\)、\(f(x) = x^2\)、\(f(x) = x^3\) 这三个简单的实例。

极值点的第二充分条件 设 \(f(x)\) 在 \(x_0\) 处二阶可导，并且 \(f'(x_0) = 0\)，\(f''(x_0) \neq 0\)，若： - \(f''(x_0) < 0\) 则 \(f(x)\) 在 \(x_0\) 取极大值。 - \(f''(x_0) > 0\) 则 \(f(x)\) 在 \(x_0\) 取极小值。

可以考虑 \(f(x) = (x + k)^2\)、\(f(x) = - (x + k)^2\) 样式的实例。

极值点的第三充分条件 设 \(f(x)\) 在 \(x_0\) 处 \(n\) 阶可导，并且 \(f'(x_0) = f''(x_0) = \cdots = f^{(n - 1)}(x_0) = 0\)，\(f^{(n)}(x_0) \neq 0\)，若： - \(n\) 为偶数，则当 \(f^(n)(x_0) < 0\) 时 \(f(x)\) 在 \(x_0\) 取极大值；当 \(f^(n)(x_0) > 0\) 时 \(f(x)\) 在 \(x_0\) 取极小值。（这是极值点的第二充分条件的推广） - \(n\) 为偶数，则 \(f(x)\) 在 \(x_0\) 处没有极值。

区间内平面曲线的凹凸性、拐点

如果函数 \(f(x)\) 在区间 \(I\) 上满足对于任意的 \(x_1,x_2 \in I\)，都有 \(\displaystyle f(\frac{x_1 + x_2}{2}) < \frac{f(x_1) + f(x_2)}{2}\)，则称函数 \(f(x)\) 在区间 \(I\) 上是凹的。

如果函数 \(f(x)\) 在区间 \(I\) 上满足对于任意的 \(x_1,x_2 \in I\)，都有 \(\displaystyle f(\frac{x_1 + x_2}{2}) > \frac{f(x_1) + f(x_2)}{2}\)，则称函数 \(f(x)\) 在区间 \(I\) 上是凸的。

如果函数 \(f(x)\) 在区间 \(I\) 上满足 \(f''(x) > 0\)，则函数 \(f(x)\) 对应的平面曲线在区间 \(I\) 上是凹的。如果函数 \(f(x)\) 在区间 \(I\) 上满足 \(f''(x) < 0\)，则函数 \(f(x)\) 对应的平面曲线在区间 \(I\) 上是凸的。

凹的曲线在曲线上连接任意两点所得到的弦在曲线的上方，曲线上任意一点的切线在曲线的下方。凸的曲线与之相反。

拐点是曲线中凹凸性发生变化的点。

驻点中非极值点的情况都是拐点。\(f(x) = x^3\) 的驻点 \((0,0)\) 是拐点。

三个充分条件可以简单地替换「在 \(x_0\) 处没有极值」与「在 \(x_0\) 处有拐点」得到。

平面曲线的曲率

有时需要定量地分析平面曲线的弯曲程度，由观察可以直观地发现：如果两条曲线的长度一样（\(=\tau\)），那么切线所转过角度较大的（\(\theta _1 > \theta _2\)）曲线弯曲地厉害；如果两条曲线切线转过的角度一样（\(=\theta\)），那么较短的（\(\tau _1 < \tau _2\)）曲线弯曲地厉害。

因此，我们将平面曲线上两点 \(M\)，\(N\) 所构成的曲线弧 \(\widetilde{MN}\) 的平均曲率定义为 \(\displaystyle \bar{k} = \frac{\theta}{\tau}\)，其中 \(\tau\) 为曲线的弧长，\(\theta\) 为曲线切线转过的角度。

当 \(\tau \rightarrow 0\) 时，若曲线弧 \(\widetilde{MN}\) 的平均曲率之极限存在，则称此极限值为曲线在 \(M\) （或者 \(N\)）点处的曲率，即 \(\displaystyle k = \lim_{\tau \rightarrow 0}\frac{\theta}{\tau}\)。

通过此定义式直接计算曲线在某点的曲率通常是不现实的，下面给出参数曲线的曲率公式以及其简要证明。

\[ \left\{ \begin{array}{lcr} \displaystyle x = \varphi(t) \\ & \Rightarrow & \displaystyle k = \frac{|\varphi''\psi' - \varphi'\psi''|}{(\varphi'^2 + \psi'^2)^{\frac{3}{2}}}\\ \displaystyle y = \psi(t) \end{array} \right. \]

对于这个公式的证明，只需要将 \(\displaystyle \frac{\Delta \alpha}{\Delta s}\) 的极限化为 \(\displaystyle \frac{d\alpha}{dt}\cdot \frac{dt}{ds}\) 即可。其中 \(ds\) 是对弧长的微分，\(\displaystyle \frac{ds}{dt} = \sqrt{\varphi'^2 + \psi'^2}\) 的证明将在第一类曲线积分中给出。

对于曲线 \(y = f(x)\)，只需令上面的 \(\varphi(t) = t\)，\(\psi(t) = f(t)\) 即可得到下面的结论：

\[ k = \frac{|(\frac{d^2}{dt^2}t)(\frac{d}{dt}f) - (\frac{d}{dt}t)(\frac{d^2}{dt^2}f)|}{[(\frac{d}{dt}t)^2 + (\frac{d}{dt}f)^2]^{\frac{3}{2}}} = \frac{|f''|}{(1 + f'^2)^{\frac{3}{2}}} \]

与导数有关的常见中英文翻译

中文	英文	含义
求导	differentiate	求极限 \(\displaystyle f'(x) = \lim_{\Delta x \rightarrow 0}\frac{f(x + \Delta x) - f(x)}{\Delta x}\)
微分	differentiate	求 \(d(f(x)) = \bigcirc dx\)
微分	differentiation	求 \(d(f(x)) = \bigcirc dx\) 的过程
微分	differential	表达式 \(d(f(x)) = \bigcirc dx\)
导数	derivative	某点的导数值 \(\displaystyle f'(x_0) = \lim_{x \rightarrow x_0}\frac{f(x) - f(x_0)}{x - x_0}\)
导函数	derivative / derivative function	关于 \(x\) 的函数 \(\displaystyle f'(x) = \lim_{\Delta x \rightarrow 0}\frac{f(x + \Delta x) - f(x)}{\Delta x}\)
可导	derivative exists	\(f'(x)\) 存在
可微	differentiable	\(\Delta y = f(x_0 + \Delta x) - f(x_0)\) 可以写成 \(A \cdot \Delta x + \omicron(\Delta x)\)

可以理解成：英文语境下并没有创造一个新的词来表达某个函数的导函数存在（即“可导”）的概念，绝大多数情况下使用“可微”一词进行替代（也许是由于对于一元函数而言，可导与可微是等价的）。

对于多元函数来说，可导的英文对照是 partially differentiable，即部分可微，也就是函数沿 x 轴或 y 轴方向的变化量可以作为一个 x 或 y 的函数存在。

这一系列相关的词语中，只有导数/导函数一词是由 derive 派生的 derivative。其他的所有词语都是从 differentiate 求微分派生的。

---

1. 参见 https://math.stackexchange.com/questions/3069969/can-fc-exist-if-fx-is-not-continuous-at-c ↩

2. Thomas University Calculus, p. 143, 643, 644 ↩

3. Thomas University Calculus, p. 212, 213, 250 ↩