词法分析：从正则表达式到确定性有穷自动机

词法分析：将输入的字符串分割为若干有意义的字串。从字符流到 Token 流。

一种词法分析器的自动生成过程是 RE - NFA - DFA。

正则表达式（Regular Expression，RE）用于形式化地描述语法。例如，C 语言的标识符 id 可以使用 RE 定义为：

digit -> 0 | 1 | 2 | ... | 9
letter_ -> _ | A | B | ... | Z | a | b | ... | z
id -> letter_ (letter_ | digit)^*

正则表达式通过最长匹配（选取最长的符合规则的子串）和规则优先（长度相同时，归类为按顺序第一个匹配的正则表达式）的规则规避二义性。

使用有穷自动机可以判定一个字符串是否被某一正则表达式描述的语法规则接受，假设有有穷自动机 \(M\)，用 \(L(M)\) 表示由所有被该有穷自动机接收的字符串组成的集合，称为由该有穷自动机接收的语言。有穷自动机分为以下两种：

它们的区别在于：

是否允许包含 \(\varepsilon-moves\)。这是一种特殊的状态转换方式，表示自动机可以不读入任何输入而将其状态由一个转换到另一个。允许包含该状态转换方式的有穷自动机称为非确定性有穷自动机 NFA 。
是否允许在状态 s 下，读入字符 'a'，存在多种状态转换方式。

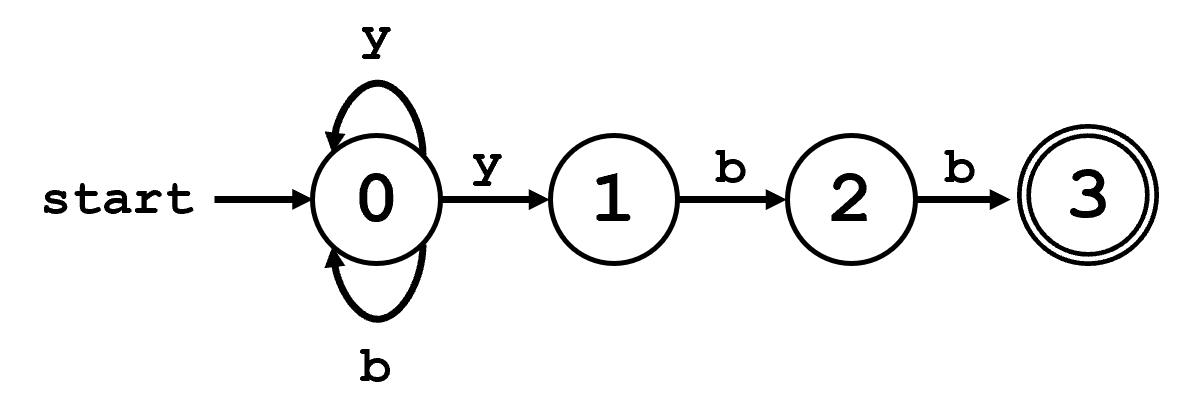
有穷自动机可以用转换图与转换表表示，下面将介绍转换图中各个基本元素的含义。

图中，每一个状态使用一个圆圈表示。

没有任何修饰的圆圈表示中间状态，例如这里的 1 和 2。

有一个无源箭头指向的圆圈表示初始/开始状态，例如这里的 0。

有两个圆圈的状态表示终止/接收状态，可以有多个，例如这里的 3。

状态之间的箭头表示状态转换，箭头上的字符串表示 FA 在进行这样的状态转换时，需要读入的字符串。特别地，用空串 \(\varepsilon\) 表示 FA 可以不读入任何输入进行此步状态转换。

上面的 FA 接收所有以 "ybb" 结尾的、字母 'y' 和 'b' 的组合。

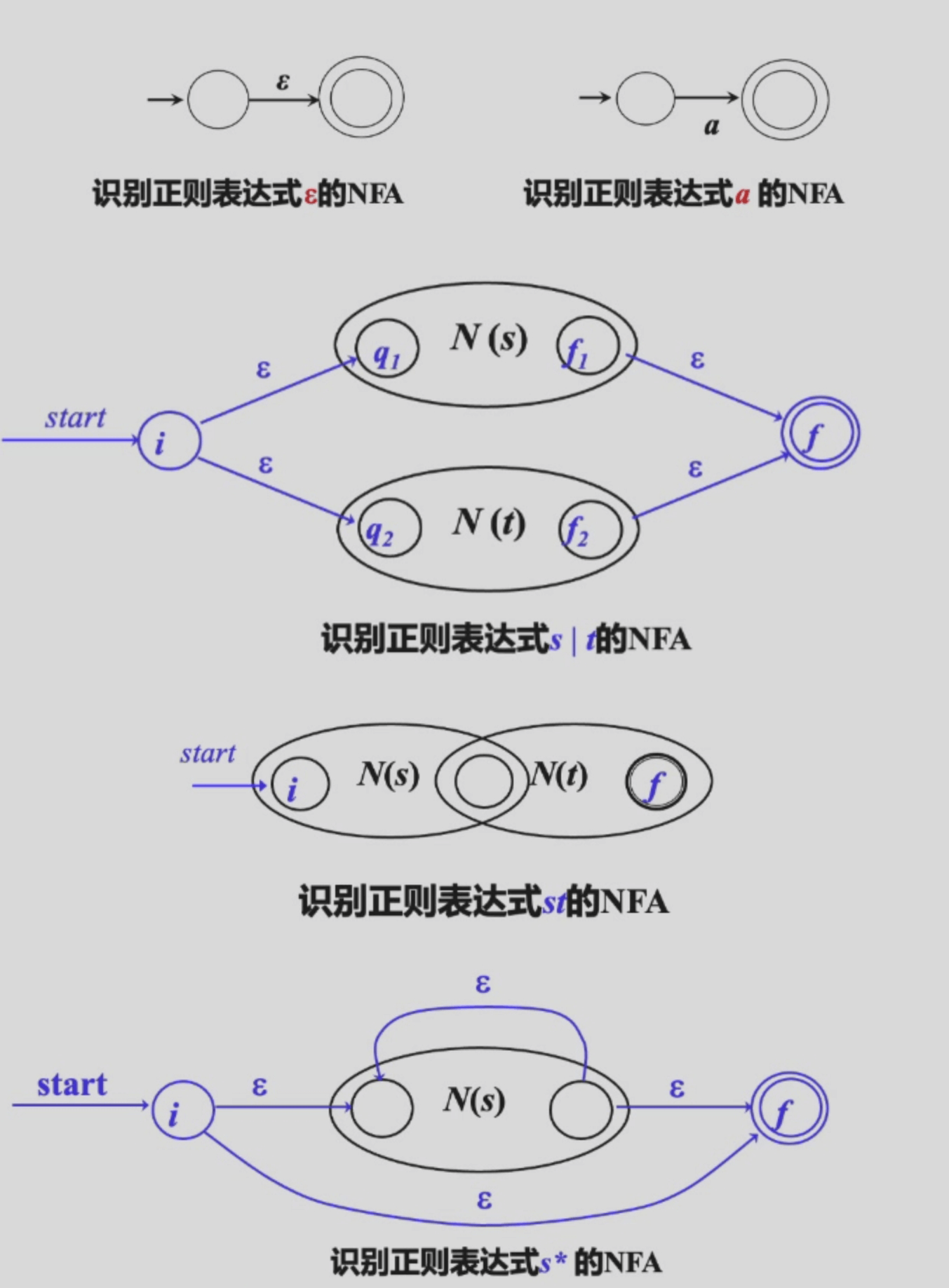
RE -> NFA 的过程的一种方法是 Thompson 算法，这种算法的本质可以类比为 PPL 中的结构归纳法：遍历所有生成 RE 的可能结构，对每种结构提出一种转换方法：

对每种结构的构造法则如下图所示¹：

NFA 在判断一个串是否被接收的时候需要多种路径试探以及失败回退，这使得它的效率非常低。

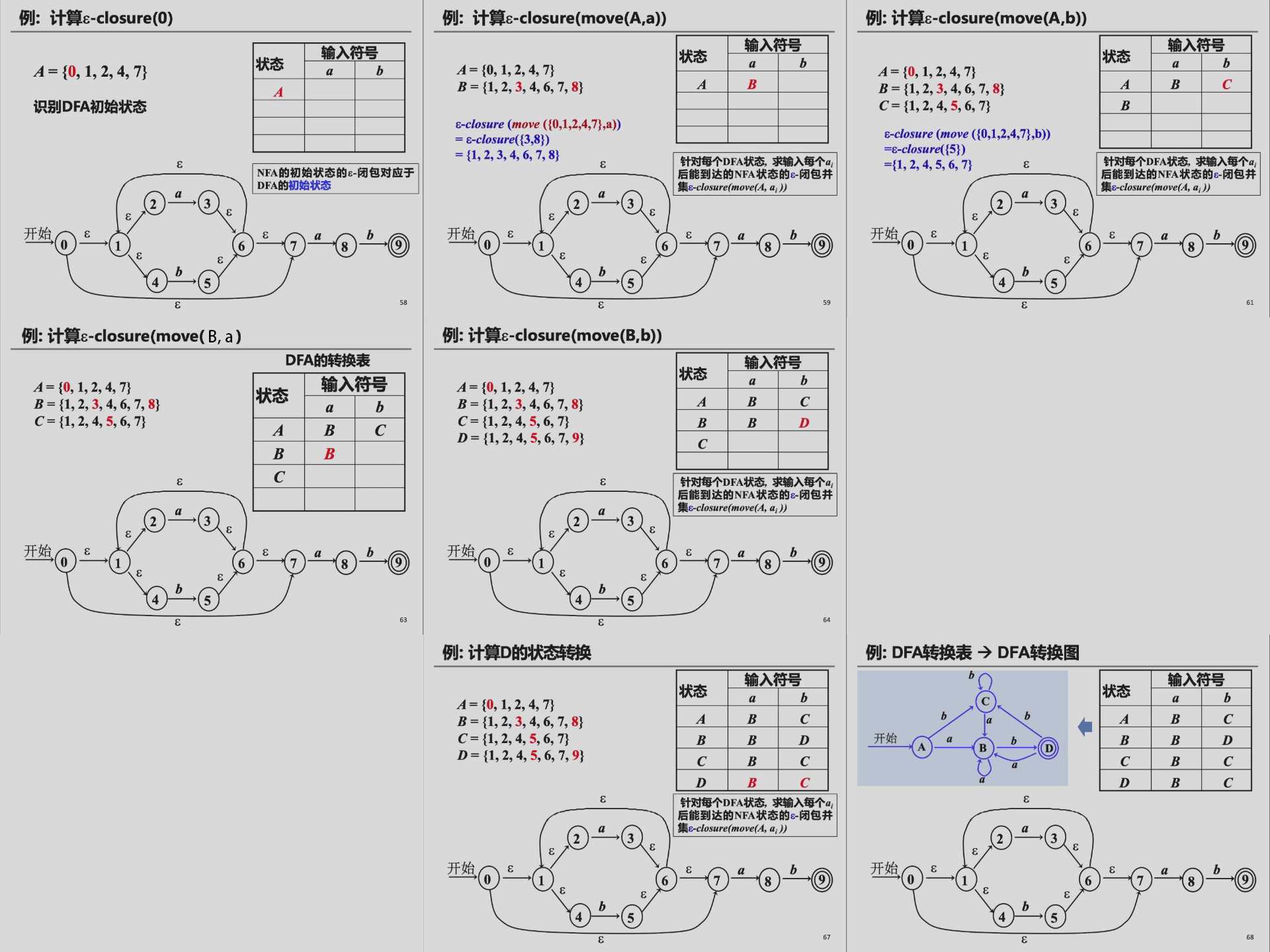
一种 NFA -> DFA 的方法是子集构造法（subset construction）。

这种方法定义了在 NFA 上的两种操作：

操作	含义	描述
\(\varepsilon-closure(s)\)	NFA 状态 \(s\) 的 \(\varepsilon\)-闭包	\(s\) 经过 \(\varepsilon\) 转换能够到达的所有状态的集合
\(\varepsilon-closure(T)\)	\(\bigcup_{s \in T} [\varepsilon-closure(s)]\)	\(T\) 中所有状态的\(\varepsilon\)-闭包之并集

子集构造法按以下过程运行：

NFA 的初始状态的 \(\varepsilon-closure\) 对应于 DFA 的初始状态。
针对已有的 DFA 的每一个状态所对应的 NFA 状态子集 \(A\)，求输入每一个 \(a_i\) 后能够到达的 NFA 状态的 \(\varepsilon-closure\) 之并集：\(\varepsilon-closure(move(A, a_i))\)。这个并集要么对应于 DFA 中的一个已有状态，要么是 DFA 中将要新加入的状态。
迭代第二步，构造 DFA 的状态转换表，直至不动点。

整个过程如下图所示¹：

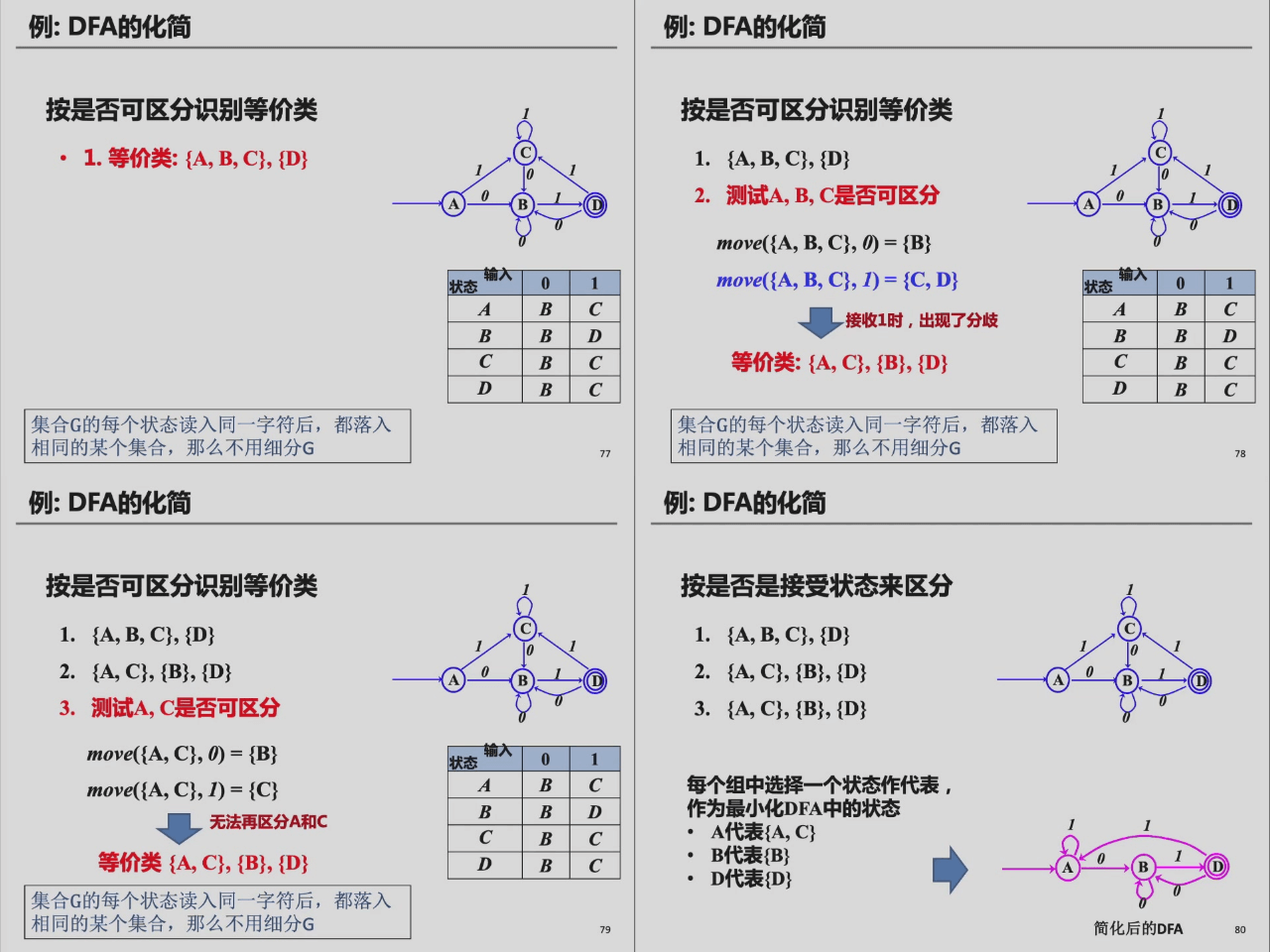
一个 RE 可以对应多个识别此 RE 对应的正则语言的 DFA，如果不计同构，则在这些 DFA 中，状态数量最小的 DFA 是唯一的。

用等价类划分的方法可以化简任何一个给定的 DFA。

这个等价类划分是指根据可区分的状态（distinguishable states）进行划分。可区分的状态是指：

如果存在串 x，使得从状态 s 与状态 t 出发，一个到达接收状态，一个到达非接收状态，则称串 x 区分了状态 s 与状态 t。

由此出发，可以得到推论：DFA 状态等价的条件：

DFA 等价算法根据上面的条件迭代地划分等价类，从划分出的等价类中选取代表重建 DFA。

初始划分为接收状态组与非接收状态组，具体流程图示如下¹：